Introduction to Smoothing Functional Data • fdars

Why Smooth Functional Data?

Real-world functional data almost always contains measurement noise. Raw observations are discrete samples of an underlying smooth process, contaminated by:

Measurement error: Instrument precision limits
Sampling noise: Random variation at each time point
Digitization artifacts: Finite resolution of recording devices

Smoothing transforms noisy discrete observations into smooth functional objects, revealing the true underlying signal. This is essential for:

Computing derivatives (noise amplifies dramatically)
Meaningful curve comparisons
Interpretable visualizations
Reliable statistical inference

library(fdars)
#> 
#> Attaching package: 'fdars'
#> The following objects are masked from 'package:stats':
#> 
#>     cov, decompose, deriv, median, sd, var
#> The following object is masked from 'package:base':
#> 
#>     norm
library(ggplot2)
theme_set(theme_minimal())
set.seed(42)

Loading Real Data: The Berkeley Growth Study

The Berkeley Growth Study tracked the heights of 54 girls and 39 boys from ages 1 to 18. This classic dataset is available in the fda package.

# Check if fda package is available
if (!requireNamespace("fda", quietly = TRUE)) {
  message("Install 'fda' package for real data examples: install.packages('fda')")
  # Create synthetic growth-like data as fallback
  age <- seq(1, 18, length.out = 31)
  n_girls <- 20
  heights <- matrix(0, n_girls, length(age))
  for (i in 1:n_girls) {
    # Gompertz growth curve with individual variation
    A <- rnorm(1, 170, 5)  # asymptotic height
    b <- rnorm(1, 2.5, 0.2)
    c <- rnorm(1, 0.15, 0.02)
    heights[i, ] <- A * exp(-b * exp(-c * age)) + rnorm(length(age), sd = 1.5)
  }
} else {
  data(growth, package = "fda")
  age <- growth$age
  heights <- t(growth$hgtf)  # Girls' heights (rows = curves, cols = time)
  n_girls <- nrow(heights)
}

# Create fdata object
fd_raw <- fdata(heights, argvals = age)
cat("Dataset:", n_girls, "growth curves measured at", length(age), "ages\n")
#> Dataset: 54 growth curves measured at 31 ages

Visualizing the Raw Data

plot(fd_raw, main = "Berkeley Growth Study: Girls' Heights",
     xlab = "Age (years)", ylab = "Height (cm)")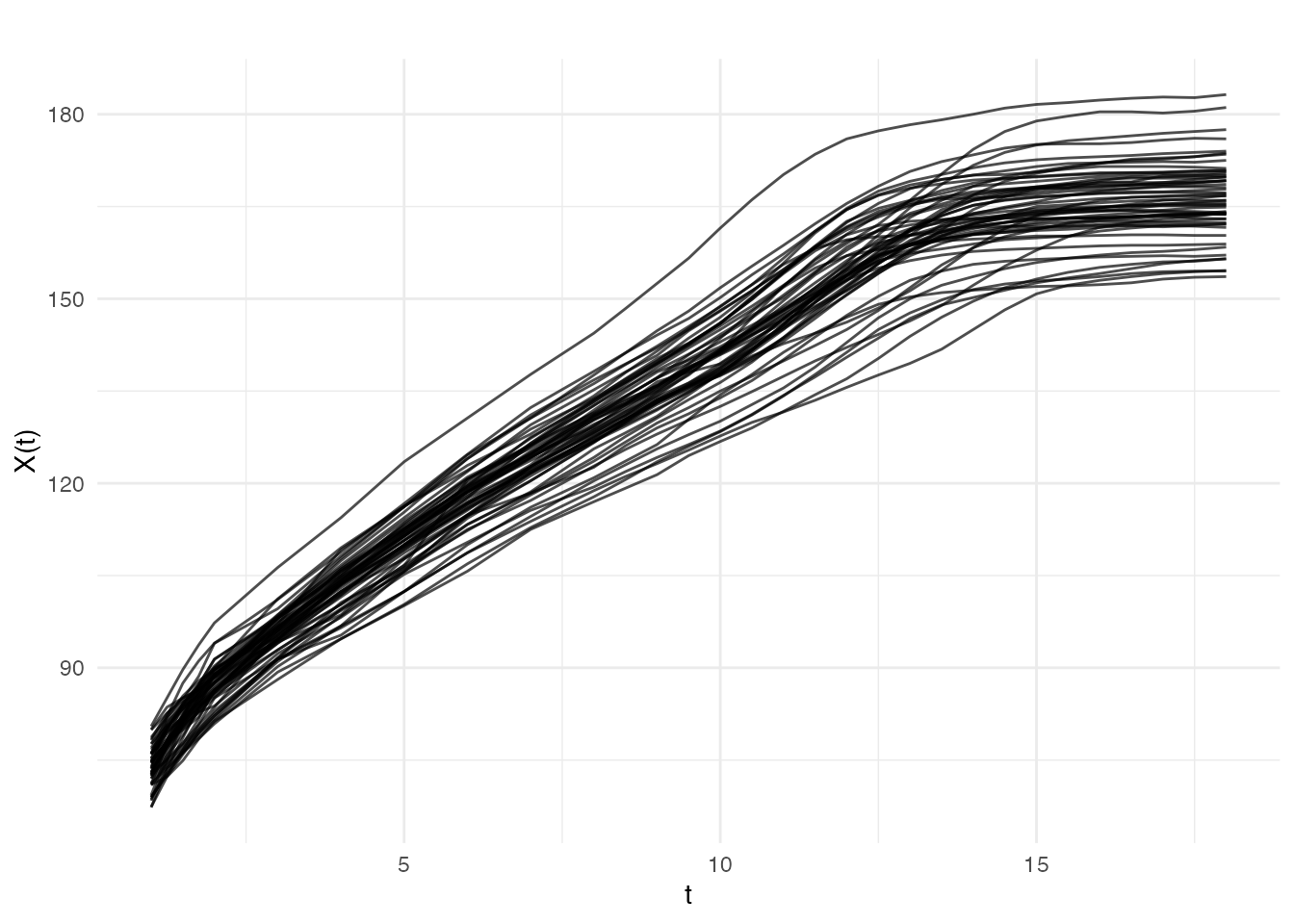

The data appears relatively smooth because height was carefully measured. Let’s add some realistic measurement noise to demonstrate smoothing techniques:

# Add measurement noise to simulate less precise instruments
noise_sd <- 2.0  # cm of measurement error
heights_noisy <- heights + matrix(rnorm(length(heights), sd = noise_sd),
                                   nrow = nrow(heights))
fd_noisy <- fdata(heights_noisy, argvals = age)

# Compare original and noisy using faceted ggplot
df_compare <- rbind(
  data.frame(
    age = rep(age, 5),
    height = as.vector(t(fd_raw$data[1:5, ])),
    curve = rep(1:5, each = length(age)),
    type = "Original"
  ),
  data.frame(
    age = rep(age, 5),
    height = as.vector(t(fd_noisy$data[1:5, ])),
    curve = rep(1:5, each = length(age)),
    type = "With Noise"
  )
)
df_compare$curve <- factor(df_compare$curve)

ggplot(df_compare, aes(x = age, y = height, color = curve)) +
  geom_line() +
  facet_wrap(~ type) +
  labs(x = "Age (years)", y = "Height (cm)", color = "Curve") +
  theme_minimal() +
  theme(legend.position = "bottom")

Method 1: P-spline Smoothing

Penalized splines (P-splines) are a powerful and flexible smoothing method. They balance two objectives:

Fit the data closely (minimize residuals)
Keep the curve smooth (penalize roughness)

The smoothing parameter $\lambda$ controls this trade-off: - Small $\lambda$ : Follows data closely, may be wiggly - Large $\lambda$ : Very smooth, may miss real features

Automatic Smoothing with P-splines

# pspline() automatically selects optimal lambda via GCV
fd_pspline <- pspline(fd_noisy)
print(fd_pspline)
#> P-spline Smoothing Results
#> ==========================
#> Number of curves: 54 
#> Number of basis functions: 20 
#> Penalty order: 2 
#> Lambda: 1e+00 
#> Effective df: 6.81 
#> GCV: 5.701e+00

Visualizing the Result

# Compare noisy vs smoothed for first curve
idx <- 1
df_pspline <- data.frame(
  age = rep(age, 3),
  height = c(fd_noisy$data[idx, ], fd_pspline$fdata$data[idx, ], fd_raw$data[idx, ]),
  type = factor(rep(c("Noisy data", "P-spline smooth", "Original"), each = length(age)),
                levels = c("Noisy data", "P-spline smooth", "Original"))
)

ggplot(df_pspline, aes(x = age, y = height, color = type, linetype = type)) +
  geom_point(data = subset(df_pspline, type == "Noisy data"),
             color = "gray60", size = 1) +
  geom_line(data = subset(df_pspline, type != "Noisy data"), linewidth = 1) +
  scale_color_manual(values = c("Noisy data" = "gray60", "P-spline smooth" = "blue",
                                 "Original" = "red")) +
  scale_linetype_manual(values = c("Noisy data" = "blank", "P-spline smooth" = "solid",
                                    "Original" = "dashed")) +
  labs(x = "Age (years)", y = "Height (cm)", title = "P-spline Smoothing",
       color = NULL, linetype = NULL) +
  theme_minimal() +
  theme(legend.position = "bottom")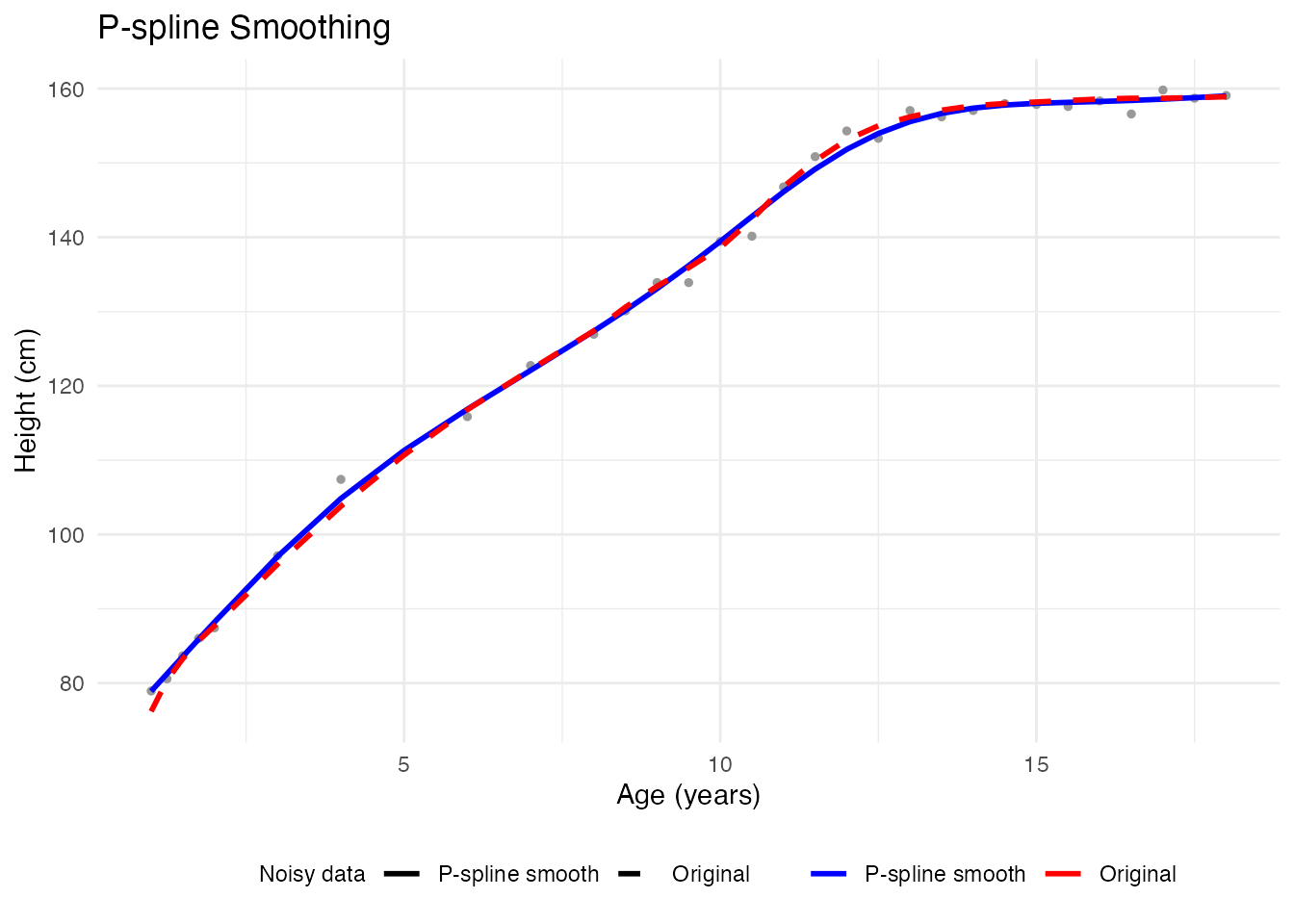

Effect of Smoothing Parameter

# Different smoothing levels
fd_less <- pspline(fd_noisy, lambda = 0.001)   # Less smoothing
fd_more <- pspline(fd_noisy, lambda = 100)     # More smoothing

idx <- 1
df_lambda <- rbind(
  data.frame(age = age, height = fd_noisy$data[idx, ], type = "data",
             lambda = "lambda = 0.001"),
  data.frame(age = age, height = fd_less$fdata$data[idx, ], type = "smooth",
             lambda = "lambda = 0.001"),
  data.frame(age = age, height = fd_noisy$data[idx, ], type = "data",
             lambda = "Optimal (GCV)"),
  data.frame(age = age, height = fd_pspline$fdata$data[idx, ], type = "smooth",
             lambda = "Optimal (GCV)"),
  data.frame(age = age, height = fd_noisy$data[idx, ], type = "data",
             lambda = "lambda = 100"),
  data.frame(age = age, height = fd_more$fdata$data[idx, ], type = "smooth",
             lambda = "lambda = 100")
)
df_lambda$lambda <- factor(df_lambda$lambda,
                            levels = c("lambda = 0.001", "Optimal (GCV)", "lambda = 100"))

ggplot(df_lambda, aes(x = age, y = height)) +
  geom_point(data = subset(df_lambda, type == "data"), color = "gray60", size = 1) +
  geom_line(data = subset(df_lambda, type == "smooth"), color = "blue", linewidth = 1) +
  facet_wrap(~ lambda) +
  labs(x = "Age (years)", y = "Height (cm)",
       title = "Effect of Smoothing Parameter") +
  theme_minimal()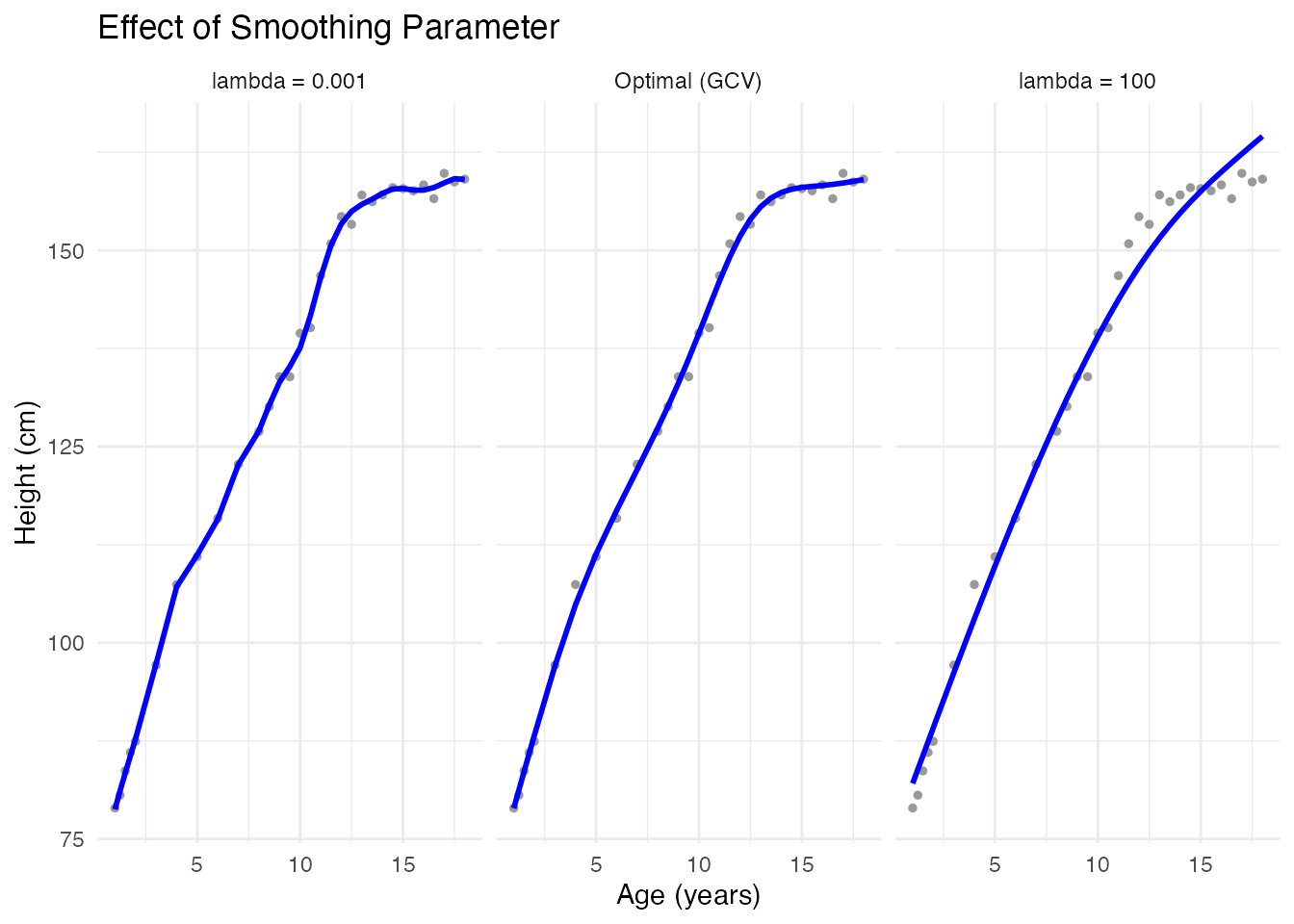

Method 2: Kernel Smoothers

Kernel smoothers estimate the value at each point using a weighted average of nearby observations. The bandwidth $h$ controls the neighborhood size.

Nadaraya-Watson Smoother

# Compute smoother matrix with Nadaraya-Watson
# S.NW takes evaluation points (tt) as first argument
h <- h.default(fd_noisy)  # Default bandwidth based on data

S_nw <- S.NW(tt = age, h = h)

# Apply smoother to each curve
fd_kernel <- fd_noisy
for (i in 1:nrow(fd_kernel$data)) {
  fd_kernel$data[i, ] <- as.vector(S_nw %*% fd_noisy$data[i, ])
}

Local Linear Regression

Local linear regression often performs better at boundaries:

S_llr <- S.LLR(tt = age, h = h)
fd_llr <- fd_noisy
for (i in 1:nrow(fd_llr$data)) {
  fd_llr$data[i, ] <- as.vector(S_llr %*% fd_noisy$data[i, ])
}

Comparing Kernel Methods

idx <- 1
df_kernels <- data.frame(
  age = rep(age, 4),
  height = c(fd_noisy$data[idx, ], fd_kernel$data[idx, ],
             fd_llr$data[idx, ], fd_raw$data[idx, ]),
  type = factor(rep(c("Data", "Nadaraya-Watson", "Local Linear", "Original"),
                    each = length(age)),
                levels = c("Data", "Nadaraya-Watson", "Local Linear", "Original"))
)

ggplot(df_kernels, aes(x = age, y = height, color = type, linetype = type)) +
  geom_point(data = subset(df_kernels, type == "Data"), size = 1) +
  geom_line(data = subset(df_kernels, type != "Data"), linewidth = 1) +
  scale_color_manual(values = c("Data" = "gray60", "Nadaraya-Watson" = "blue",
                                 "Local Linear" = "darkgreen", "Original" = "red")) +
  scale_linetype_manual(values = c("Data" = "blank", "Nadaraya-Watson" = "solid",
                                    "Local Linear" = "solid", "Original" = "dashed")) +
  labs(x = "Age (years)", y = "Height (cm)",
       title = "Kernel Smoother Comparison", color = NULL, linetype = NULL) +
  theme_minimal() +
  theme(legend.position = "bottom")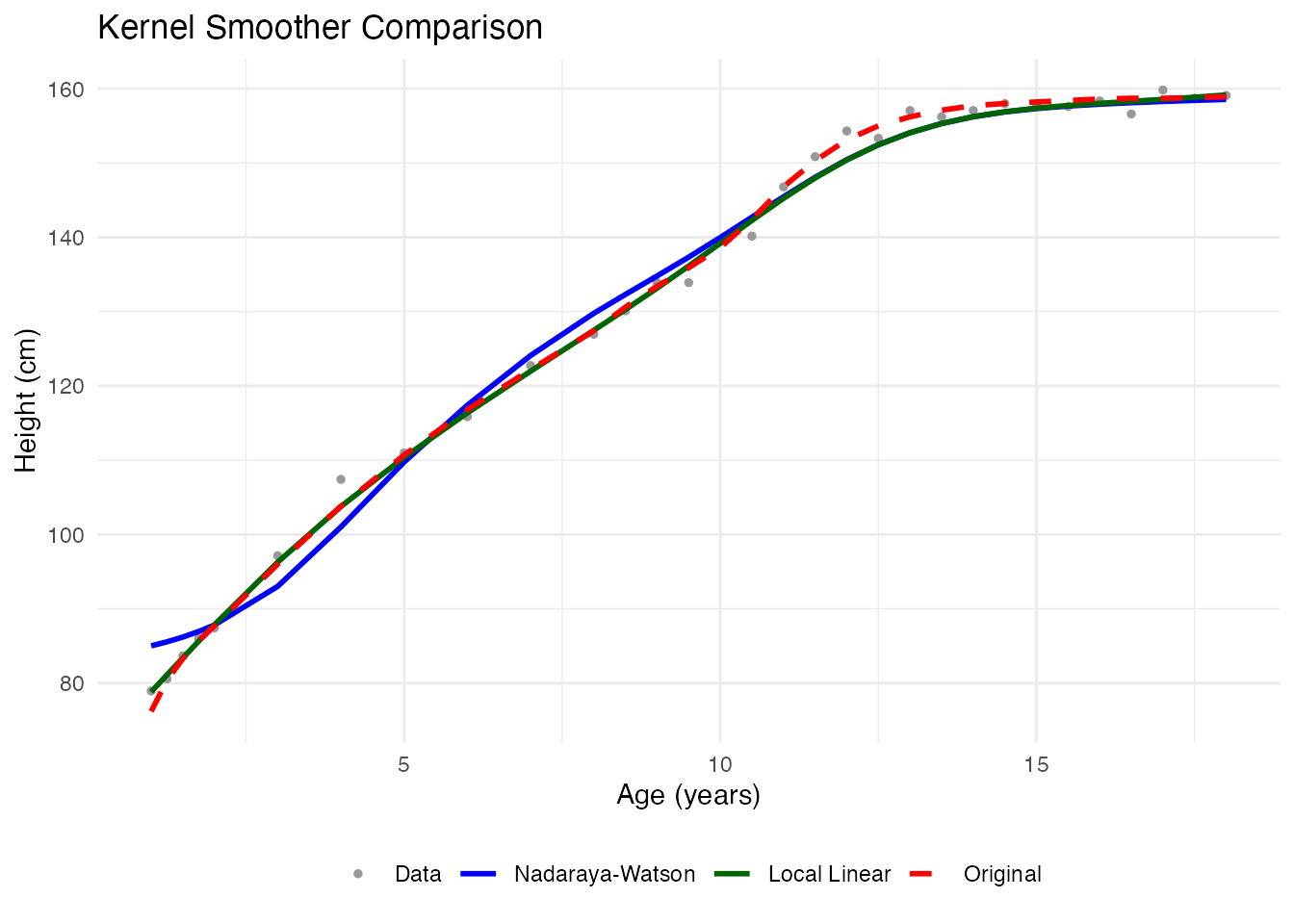

Bandwidth Selection

The default bandwidth from h.default() is based on the data:

cat("Default bandwidth:", h, "\n")
#> Default bandwidth: 1.5
cat("This is computed as the 15th percentile of pairwise distances.\n")
#> This is computed as the 15th percentile of pairwise distances.

Method 3: Basis Expansion

Represent curves as linear combinations of basis functions. This provides dimensionality reduction along with smoothing.

B-spline Basis

# Project to B-spline basis
coefs <- fdata2basis(fd_noisy, nbasis = 12, type = "bspline")
fd_basis <- basis2fdata(coefs, argvals = age, type = "bspline")

# Compare
idx <- 1
df_bspline <- data.frame(
  age = rep(age, 3),
  height = c(fd_noisy$data[idx, ], fd_basis$data[idx, ], fd_raw$data[idx, ]),
  type = factor(rep(c("Data", "B-spline", "Original"), each = length(age)),
                levels = c("Data", "B-spline", "Original"))
)

ggplot(df_bspline, aes(x = age, y = height, color = type, linetype = type)) +
  geom_point(data = subset(df_bspline, type == "Data"), size = 1) +
  geom_line(data = subset(df_bspline, type != "Data"), linewidth = 1) +
  scale_color_manual(values = c("Data" = "gray60", "B-spline" = "purple",
                                 "Original" = "red")) +
  scale_linetype_manual(values = c("Data" = "blank", "B-spline" = "solid",
                                    "Original" = "dashed")) +
  labs(x = "Age (years)", y = "Height (cm)", title = "B-spline Basis (K=12)",
       color = NULL, linetype = NULL) +
  theme_minimal() +
  theme(legend.position = "bottom")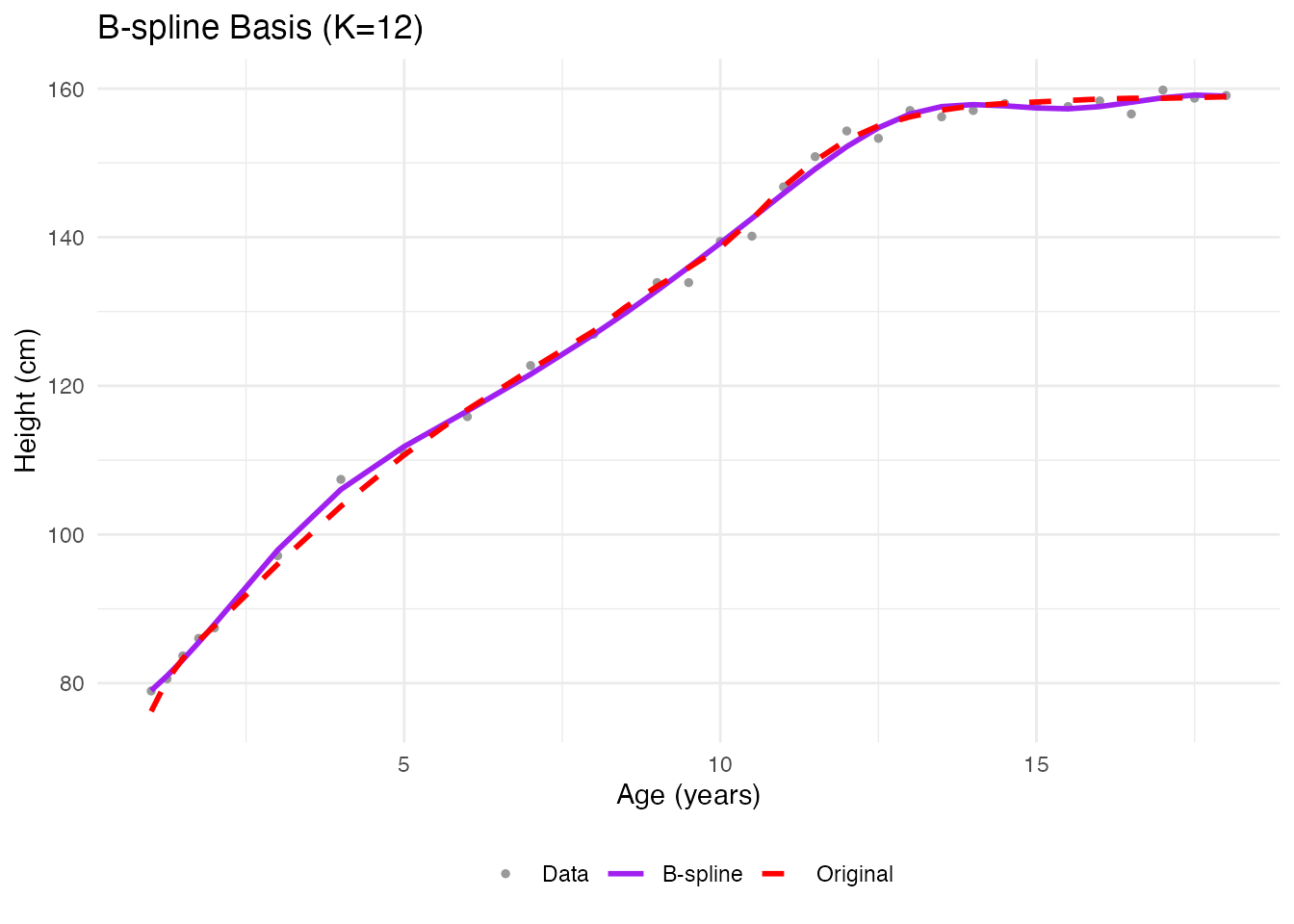

Automatic Basis Selection

How many basis functions? Cross-validation finds the optimal number:

# Cross-validation for optimal number of basis functions
cv_basis <- fdata2basis_cv(fd_noisy, type = "bspline",
                           nbasis.range = 5:20)
print(cv_basis)
#> Basis Cross-Validation Results
#> ==============================
#> Criterion: GCV 
#> Optimal nbasis: 11 
#> Score at optimal: 5.906161 
#> Range tested: 5 - 20
plot(cv_basis)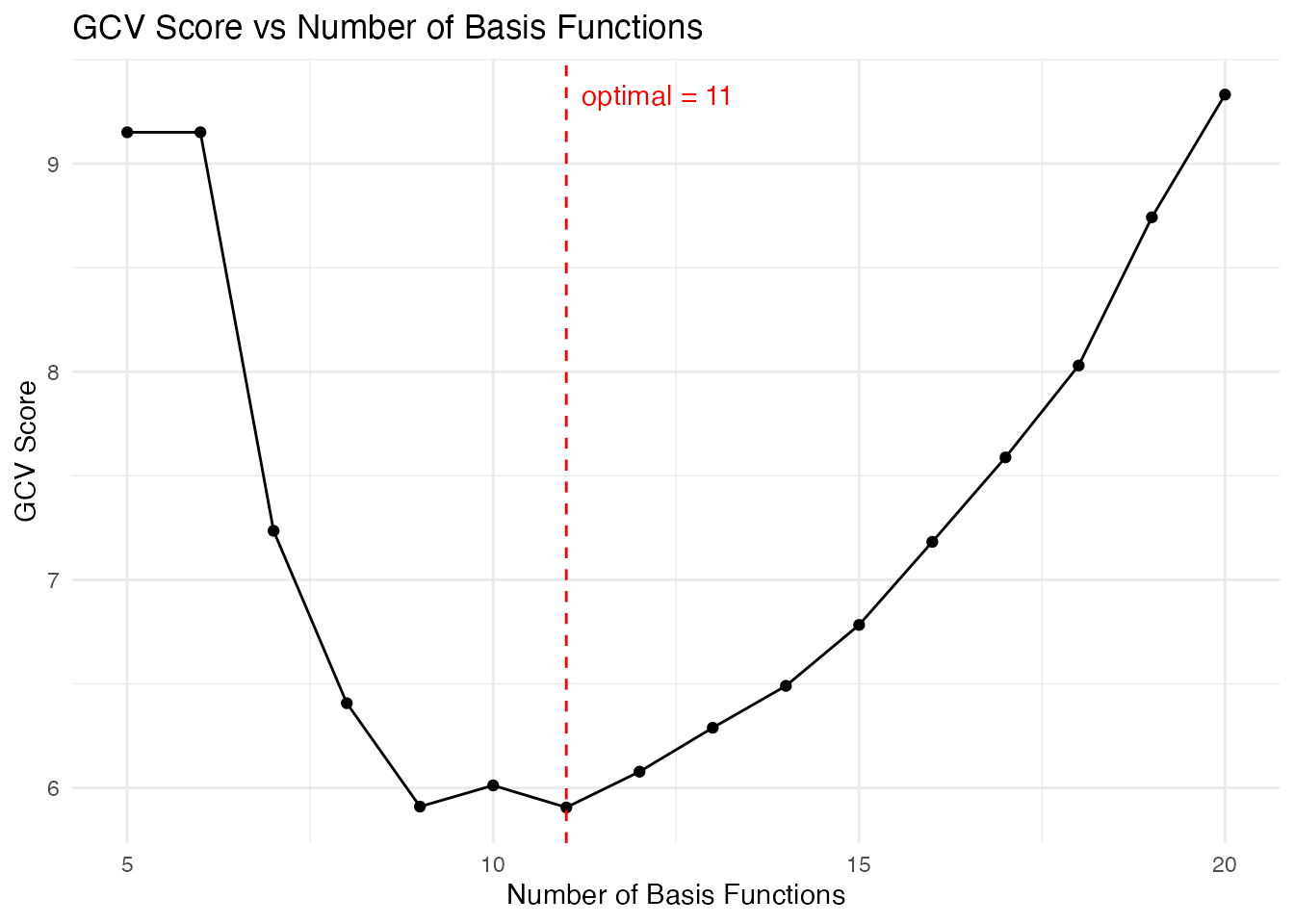

Information Criteria

The fdata2basis_cv function supports different criteria: - GCV (default): Generalized Cross-Validation - CV: Leave-one-out Cross-Validation - AIC: Akaike Information Criterion - BIC: Bayesian Information Criterion

# Get optimal basis from our CV result
optimal_nbasis <- cv_basis$optimal.nbasis
cat("Optimal number of basis functions (GCV):", optimal_nbasis, "\n")
#> Optimal number of basis functions (GCV): 11

Comparing All Methods

idx <- 3  # Pick a different curve

# Get smoothed versions
smooth_pspline <- fd_pspline$fdata$data[idx, ]
smooth_kernel <- fd_llr$data[idx, ]

# Use optimal basis from CV
coefs_opt <- fdata2basis(fd_noisy, nbasis = optimal_nbasis, type = "bspline")
smooth_basis <- basis2fdata(coefs_opt, argvals = age, type = "bspline")$data[idx, ]

# Create data frame for plotting
df_all <- data.frame(
  age = rep(age, 5),
  height = c(fd_noisy$data[idx, ], smooth_pspline, smooth_kernel,
             smooth_basis, fd_raw$data[idx, ]),
  method = factor(rep(c("Noisy data", "P-spline", "Local Linear",
                        "B-spline basis", "Original"), each = length(age)),
                  levels = c("Noisy data", "P-spline", "Local Linear",
                             "B-spline basis", "Original"))
)

ggplot(df_all, aes(x = age, y = height, color = method, linetype = method)) +
  geom_point(data = subset(df_all, method == "Noisy data"), size = 1) +
  geom_line(data = subset(df_all, method != "Noisy data"), linewidth = 1) +
  scale_color_manual(values = c("Noisy data" = "gray60", "P-spline" = "blue",
                                 "Local Linear" = "darkgreen", "B-spline basis" = "purple",
                                 "Original" = "red")) +
  scale_linetype_manual(values = c("Noisy data" = "blank", "P-spline" = "solid",
                                    "Local Linear" = "solid", "B-spline basis" = "solid",
                                    "Original" = "dashed")) +
  labs(x = "Age (years)", y = "Height (cm)",
       title = "Smoothing Method Comparison", color = NULL, linetype = NULL) +
  theme_minimal() +
  theme(legend.position = "bottom")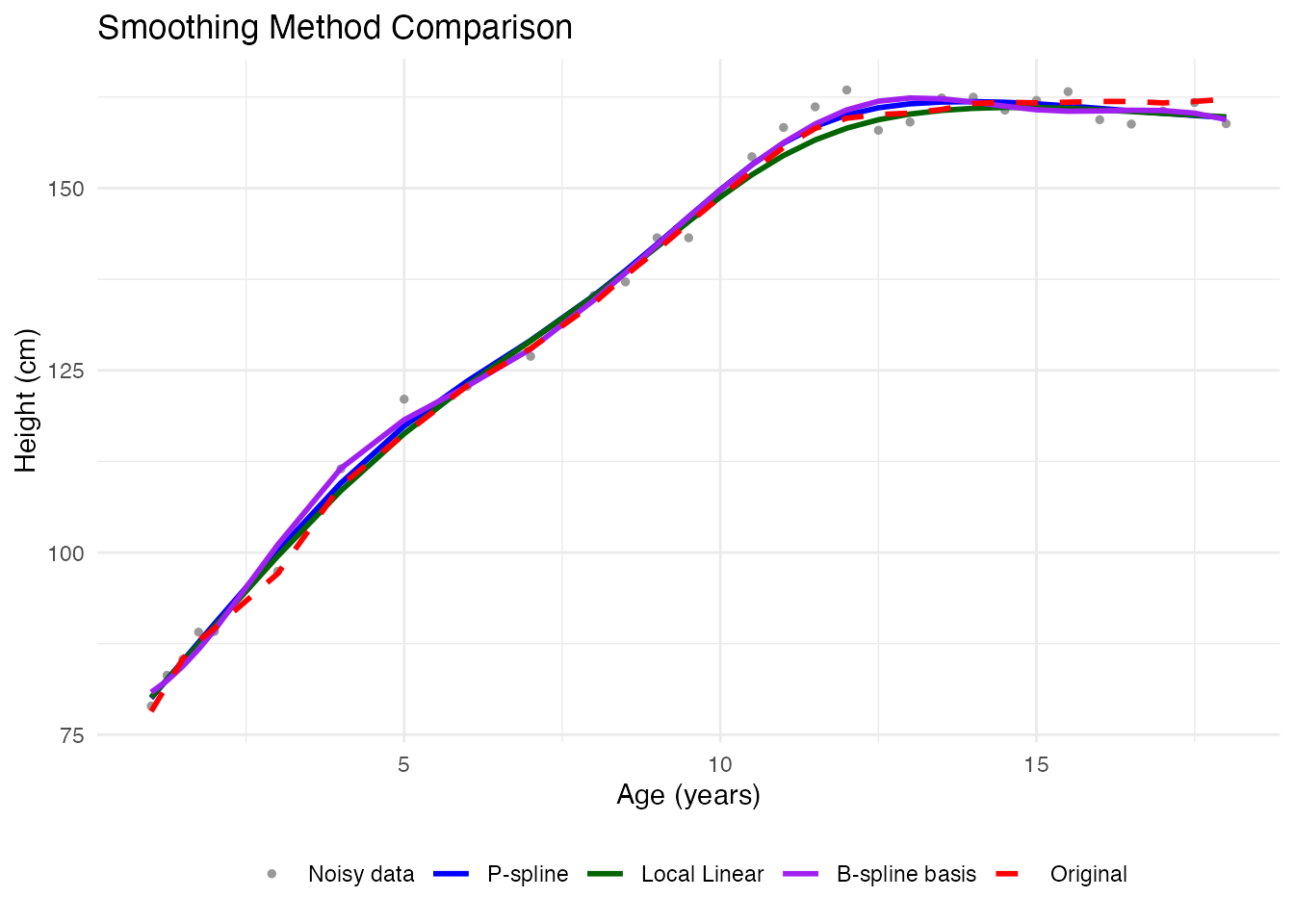

Mean and Variability

After smoothing, compute summary statistics:

# Use P-spline smoothed data
fd_smooth <- fd_pspline$fdata

# Mean curve
mean_curve <- mean(fd_smooth)

# Standard deviation at each point
sd_curve <- sd(fd_smooth)

# Create data frame for plotting
df_mean <- data.frame(
  age = age,
  mean = mean_curve$data[1, ],
  lower = mean_curve$data[1, ] - 2 * sd_curve$data[1, ],
  upper = mean_curve$data[1, ] + 2 * sd_curve$data[1, ]
)

ggplot(df_mean, aes(x = age)) +
  geom_ribbon(aes(ymin = lower, ymax = upper), fill = "blue", alpha = 0.2) +
  geom_line(aes(y = mean), color = "blue", linewidth = 1.2) +
  labs(x = "Age (years)", y = "Height (cm)",
       title = "Mean Growth Curve with Variability Band",
       subtitle = "Shaded region: Mean +/- 2 SD") +
  theme_minimal()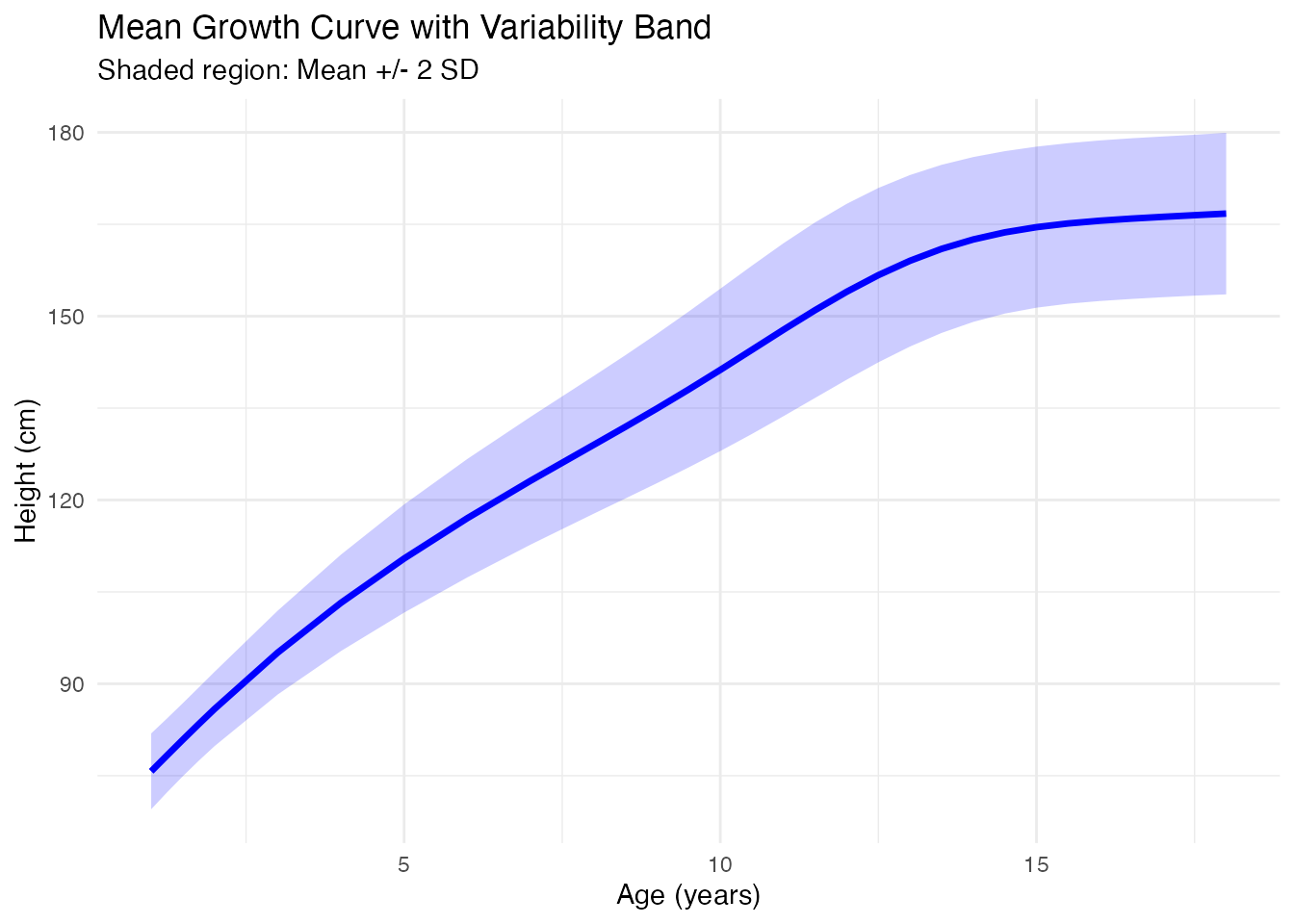

Summary: When to Use Each Method

Method	Best For	Key Parameter
P-splines	General purpose, automatic tuning	$\lambda$ (smoothing)
Kernel smoothers	Non-parametric, local adaptation	$h$ (bandwidth)
Basis expansion	Dimensionality reduction, derivatives	$K$ (number of basis)

Recommendations:

Start with P-splines - automatic $\lambda$ selection works well in most cases
Use basis expansion when you need derivatives (smoother derivatives)
Use kernel smoothers for highly irregular sampling or adaptive smoothing

References

Ramsay, J.O. and Silverman, B.W. (2005). Functional Data Analysis. Springer.
Eilers, P.H.C. and Marx, B.D. (1996). Flexible Smoothing with B-splines and Penalties. Statistical Science, 11(2), 89-121.
Fan, J. and Gijbels, I. (1996). Local Polynomial Modelling and Its Applications. Chapman and Hall.