Outlier Detection • fdars

Introduction

Outlier detection in functional data identifies curves that are atypical or anomalous compared to the rest of the sample. fdars provides several methods based on functional depth and likelihood ratio tests.

library(fdars)
#> 
#> Attaching package: 'fdars'
#> The following objects are masked from 'package:stats':
#> 
#>     cov, decompose, deriv, median, sd, var
#> The following object is masked from 'package:base':
#> 
#>     norm
library(ggplot2)
theme_set(theme_minimal())

# Generate normal data with low noise for clear signal
set.seed(42)
n <- 30
m <- 100
t_grid <- seq(0, 1, length.out = m)

X <- matrix(0, n, m)
for (i in 1:n) {
  X[i, ] <- sin(2 * pi * t_grid) + rnorm(m, sd = 0.1)
}

# Add three distinct types of outliers
X[1, ] <- sin(2 * pi * t_grid) + 3           # MAGNITUDE outlier (shifted up)
X[2, ] <- -sin(2 * pi * t_grid)              # SHAPE outlier (inverted pattern)
X[3, ] <- 3 * sin(2 * pi * t_grid)           # AMPLITUDE outlier (larger scale)

fd <- fdata(X, argvals = t_grid)

# Visualize with outliers highlighted
df_curves <- data.frame(
  t = rep(t_grid, n),
  value = as.vector(t(X)),
  curve = rep(1:n, each = m),
  type = rep(c("Magnitude", "Shape", "Amplitude", rep("Normal", n - 3)), each = m)
)
df_curves$type <- factor(df_curves$type, levels = c("Normal", "Magnitude", "Shape", "Amplitude"))

ggplot(df_curves, aes(x = t, y = value, group = curve, color = type)) +
  geom_line(alpha = 0.7) +
  scale_color_manual(values = c("Normal" = "gray50", "Magnitude" = "red",
                                 "Shape" = "blue", "Amplitude" = "green3")) +
  labs(title = "Functional Data with Three Types of Outliers",
       x = "t", y = "X(t)", color = "Type") +
  theme(legend.position = "bottom")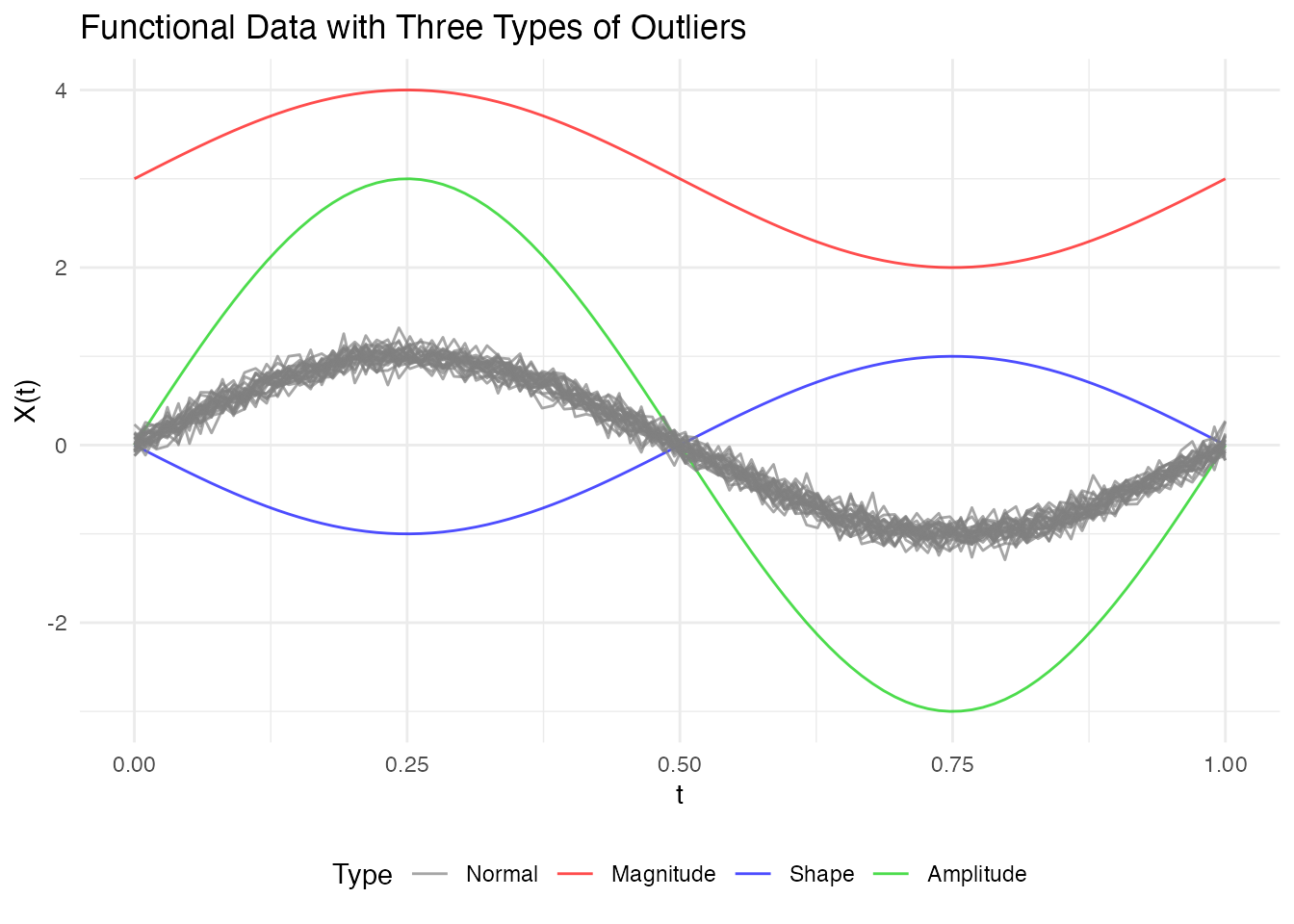

Depth-Based Methods

Depth-based outlier detection identifies curves with unusually low depth (far from the center of the data).

Weighted Depth Method (outliers.depth.pond)

Uses bootstrap resampling to estimate the distribution of depths and identifies curves with depth below a data-driven cutoff. The function supports three different methods for computing the threshold.

Threshold Methods

Method	Formula	When to Use
`"quantile"`	`quantile(depths, quan)`	When you expect a specific proportion of outliers
`"mad"`	`median - k × MAD`	More robust when outliers may already exist
`"iqr"`	`Q1 - k × IQR`	Boxplot-style detection

Default: 95th percentile threshold (quan = 0.05), which flags curves in the bottom 5% of depths as outliers.

# Default: quantile method with quan = 0.05 (95th percentile, flags bottom 5%)
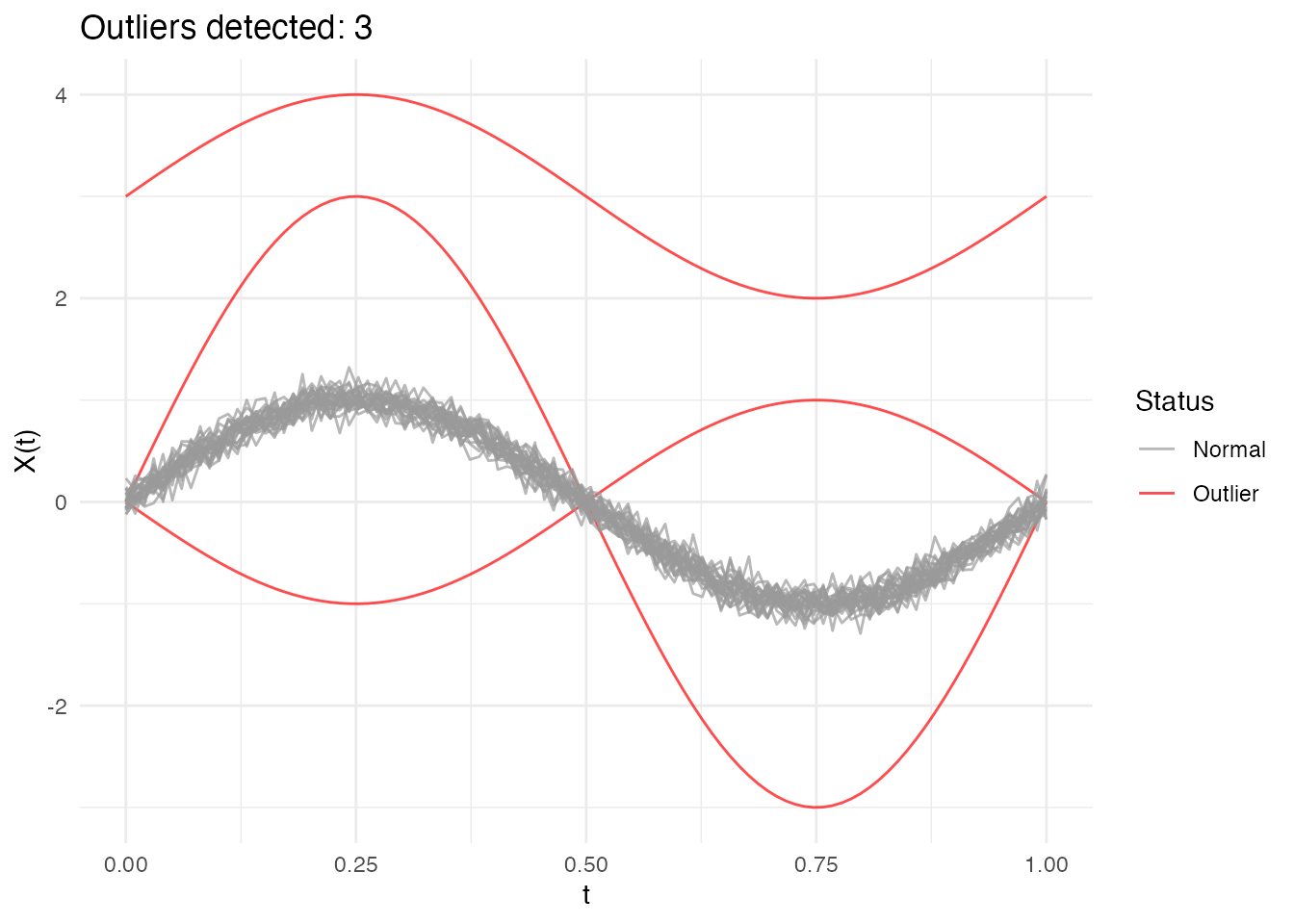
out_pond <- outliers.depth.pond(fd, nb = 1000)
print(out_pond)
#> Functional data outlier detection
#>   Number of observations: 30 
#>   Number of outliers: 3 
#>   Outlier indices: 1 2 3
#>   Threshold method: quantile 
#>   Depth cutoff: 0.0591

Comparing Threshold Methods

# Quantile method: flags curves with depth in the bottom 5% (default)
out_quantile <- outliers.depth.pond(fd, nb = 1000,
                                     threshold_method = "quantile", quan = 0.05)
cat("Quantile (5%): ", out_quantile$outliers, "\n")
#> Quantile (5%):  1 2 3

# More permissive: bottom 10%
out_quantile10 <- outliers.depth.pond(fd, nb = 1000,
                                       threshold_method = "quantile", quan = 0.1)
cat("Quantile (10%):", out_quantile10$outliers, "\n")
#> Quantile (10%): 1 2 3

# MAD method: more robust, uses median - 2.5*MAD
out_mad <- outliers.depth.pond(fd, nb = 1000,
                                threshold_method = "mad", k = 2.5)
cat("MAD (k=2.5):   ", out_mad$outliers, "\n")
#> MAD (k=2.5):    1 2 3

# IQR method: boxplot-like, uses Q1 - 1.5*IQR
out_iqr <- outliers.depth.pond(fd, nb = 1000,
                                threshold_method = "iqr", k = 1.5)
cat("IQR (k=1.5):   ", out_iqr$outliers, "\n")
#> IQR (k=1.5):    1 2 3

Choosing the right method:

Quantile (default): Uses a fixed proportion cutoff. The default quan = 0.05 (95th percentile) flags the bottom 5% of curves. Increase to quan = 0.1 for more permissive detection.
MAD: More robust to existing outliers in the data. The default k = 2.5 corresponds roughly to a 1-2% false positive rate. Increase k for stricter detection (fewer outliers).
IQR: Similar to boxplot fences. The default k = 1.5 is the standard boxplot rule. Use k = 3.0 for “far outliers” only.

Visualizing Outliers

plot(out_pond)

Examining Results

# Which curves are outliers?
out_pond$outliers
#> [1] 1 2 3

# Depth values for all curves
head(out_pond$depths)
#> [1] 0.03333337 0.05506193 0.05477837 0.87274161 0.86959674 0.86759472

# Cutoff used
cat("Cutoff:", out_pond$cutoff, "\n")
#> Cutoff: 0.05905061
cat("Threshold method:", out_pond$threshold_method, "\n")
#> Threshold method: quantile

Understanding depth.pond Results

The outliers.depth.pond method uses bootstrap resampling to estimate what depth values are “normal” for your dataset.

Key behaviors:

Edge curves: Curves near the boundary of the data cloud naturally have lower depth, even if they’re not true outliers
Bootstrap variability: Small samples give unstable cutoffs - use at least nb = 200 for stable results
Threshold choice matters: The quantile method with a fixed proportion will always flag that proportion as outliers. Use mad or iqr for data-driven thresholds that adapt to the actual depth distribution.

Recommendation: Start with threshold_method = "mad" for a robust, data-driven approach. Adjust k based on how conservative you want the detection to be.

Compare with outliers.depth.trim which uses a fixed trim proportion - more predictable but requires you to choose the proportion.

Trimming-Based Method (outliers.depth.trim)

Iteratively removes curves with lowest depth:

out_trim <- outliers.depth.trim(fd, trim = 0.1, seed = 123)
print(out_trim)
#> Functional data outlier detection
#>   Number of observations: 30 
#>   Number of outliers: 3 
#>   Outlier indices: 1 2 3
#>   Depth cutoff: 0.7817
plot(out_trim)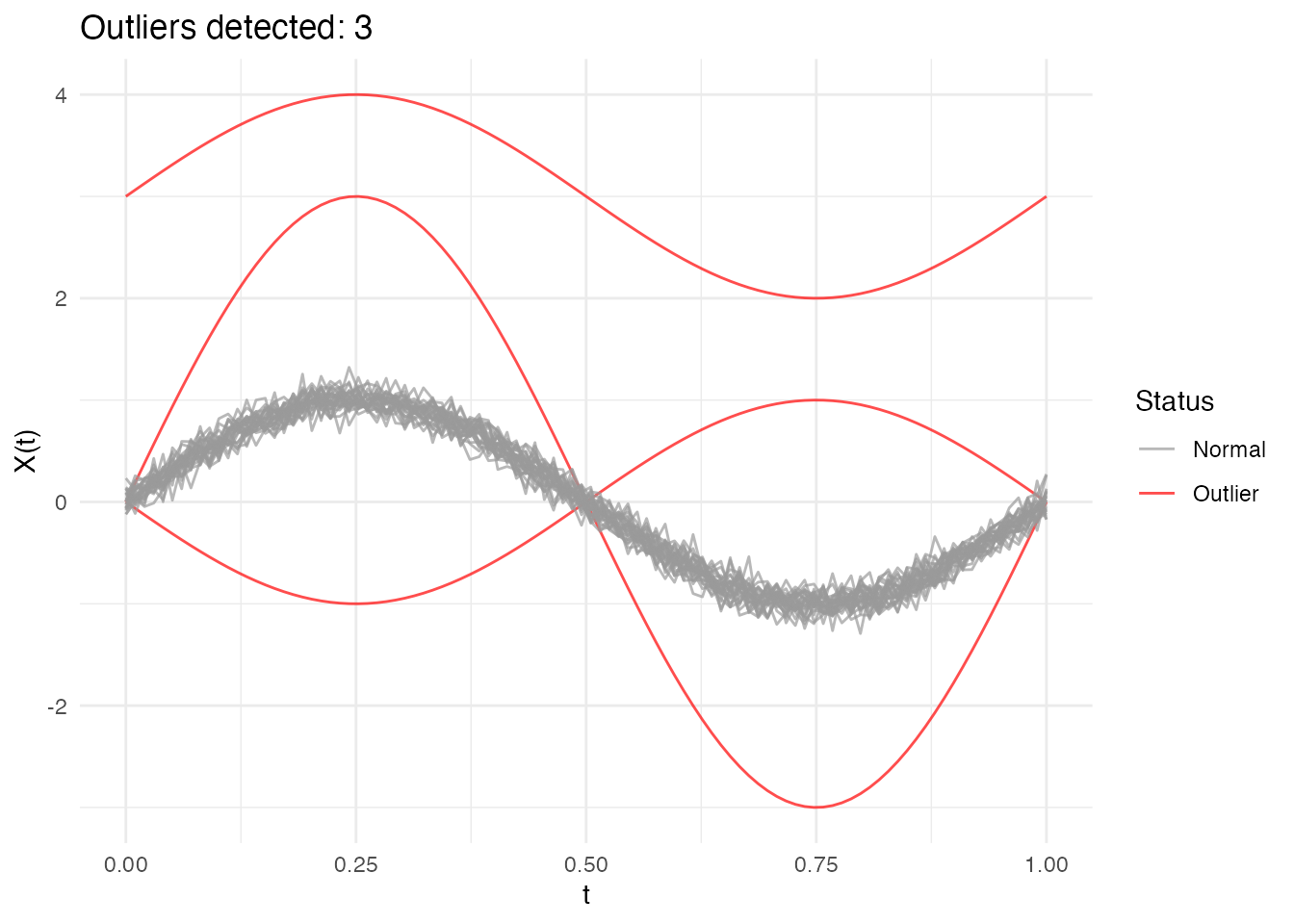

Using Different Depth Functions

Both methods accept a depth parameter to specify the depth function:

# Using Random Projection depth
out_rp <- outliers.depth.pond(fd, nb = 1000, seed = 123)

# Using modal depth (default is FM)
out_mode <- outliers.depth.trim(fd, trim = 0.1, seed = 123)

Likelihood Ratio Test (LRT) Method

The LRT method uses a likelihood ratio test to sequentially identify outliers. It’s particularly effective for detecting magnitude outliers.

Automatic Threshold Computation

The LRT method automatically computes a bootstrap threshold based on a percentile of the maximum distance distribution under the null hypothesis (no outliers). By default, the 99th percentile is used, meaning approximately 1% of observations would be flagged as outliers when there are no true outliers.

# The outliers.lrt function automatically computes the threshold
out_lrt <- outliers.lrt(fd, nb = 1000, seed = 123)
print(out_lrt)
#> Functional data outlier detection
#>   Number of observations: 30 
#>   Number of outliers: 0 
#>   LRT threshold: 32.913  (99th percentile)
plot(out_lrt)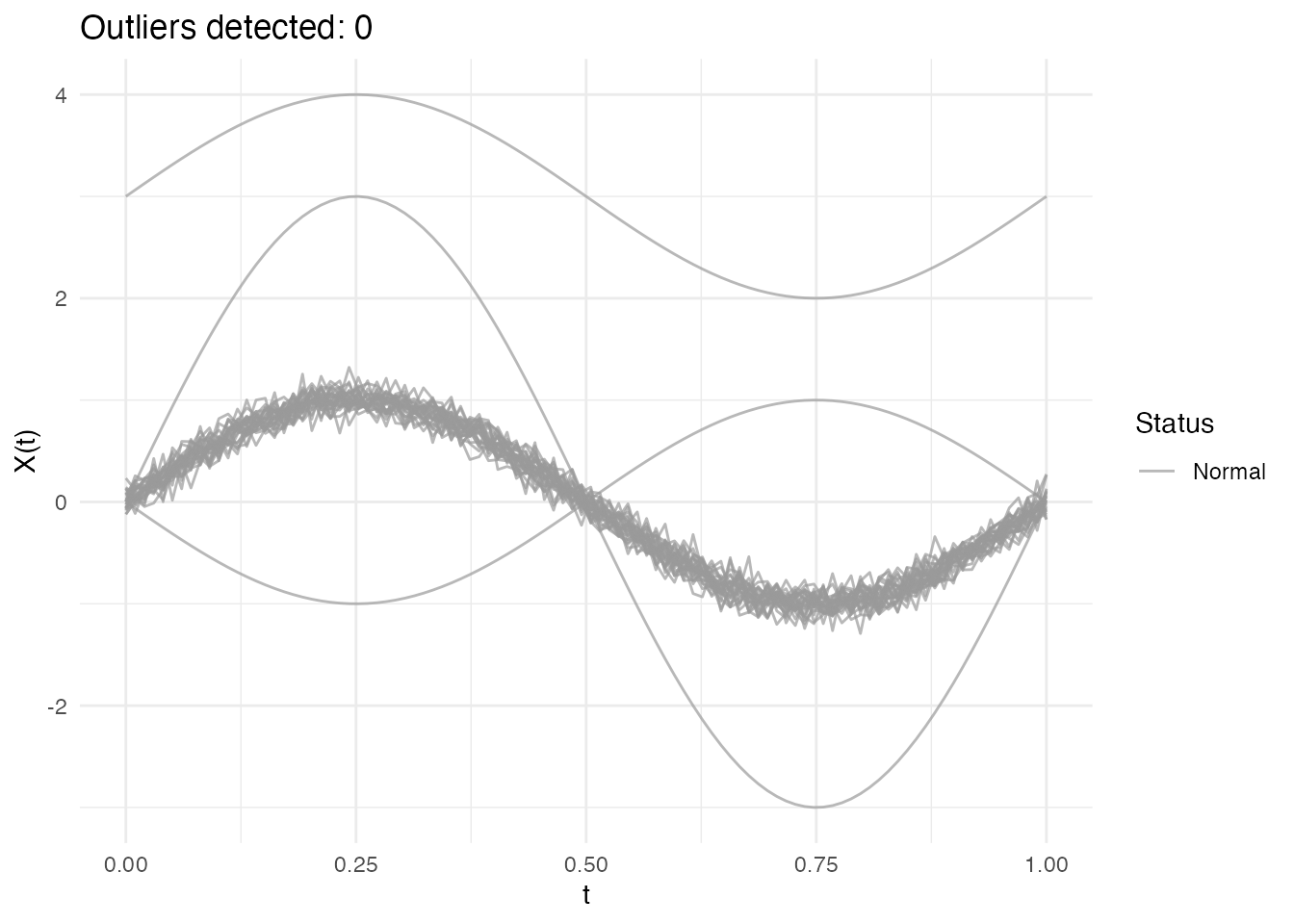

Configuring the Percentile

The percentile parameter controls the sensitivity of the LRT method:

Higher percentile (e.g., 0.99): More conservative, fewer false positives
Lower percentile (e.g., 0.95): More sensitive, may catch more subtle outliers

# Default: 99th percentile (conservative)
out_lrt_99 <- outliers.lrt(fd, nb = 1000, seed = 123, percentile = 0.99)
cat("99th percentile outliers:", out_lrt_99$outliers, "\n")
#> 99th percentile outliers:

# More sensitive: 95th percentile
out_lrt_95 <- outliers.lrt(fd, nb = 1000, seed = 123, percentile = 0.95)
cat("95th percentile outliers:", out_lrt_95$outliers, "\n")
#> 95th percentile outliers:

Manual Threshold Computation

You can also compute the threshold separately if you want to examine it or apply a custom threshold:

# Compute threshold separately (99th percentile by default)
threshold_99 <- outliers.thres.lrt(fd, nb = 1000, seed = 123)
cat("LRT threshold (99th percentile):", threshold_99, "\n")
#> LRT threshold (99th percentile): 32.91297

# Or with a different percentile
threshold_95 <- outliers.thres.lrt(fd, nb = 1000, seed = 123, percentile = 0.95)
cat("LRT threshold (95th percentile):", threshold_95, "\n")
#> LRT threshold (95th percentile): 32.36814

LRT Results

# Outlier indices
out_lrt$outliers
#> integer(0)

# Distance from center for each curve
head(out_lrt$distances)
#> [1] 31.2933479 14.5221905 14.5627739  0.8885643  0.9423256  1.0432319

# Threshold used
out_lrt$threshold
#> [1] 32.91297

When LRT Works Best

The LRT method is specifically optimized for magnitude outliers - curves that are shifted up or down relative to the main data cloud. It computes how far each curve is from the center (mean) of the data.

What LRT detects well: - Curves shifted up or down (magnitude outliers) - Curves with unusual overall level

What LRT may miss: - Shape outliers (different pattern but similar overall level) - Amplitude outliers (scaled versions centered at the same level)

Using the threshold (outliers.thres.lrt()):

The threshold represents the critical value of the LRT statistic. Use it to:

Apply a custom significance level
Compare test statistics across different datasets
Combine with domain knowledge for decision-making

If LRT detects no outliers when you expect some: 1. The outliers may be shape-based rather than magnitude-based 2. Try depth-based methods (outliers.depth.pond or outliers.depth.trim) instead 3. Use the outliergram or MS-plot for visual detection

Comparing Methods

Different methods may detect different types of outliers:

# Run all methods
out1 <- outliers.depth.pond(fd, nb = 1000, seed = 123)
out2 <- outliers.depth.trim(fd, trim = 0.1, seed = 123)
out3 <- outliers.lrt(fd, nb = 1000, seed = 123)

# Compare detected outliers
cat("Depth-pond outliers:", out1$outliers, "\n")
#> Depth-pond outliers: 1 2 3
cat("Depth-trim outliers:", out2$outliers, "\n")
#> Depth-trim outliers: 1 2 3
cat("LRT outliers:", out3$outliers, "\n")
#> LRT outliers:

# True outliers are curves 1, 2, 3
cat("True outliers: 1, 2, 3\n")
#> True outliers: 1, 2, 3

Types of Outliers

Magnitude Outliers

Curves shifted up or down from the main group:

# Create clean data with just a magnitude outlier
X_mag <- matrix(0, n, m)
for (i in 1:n) {
  X_mag[i, ] <- sin(2 * pi * t_grid) + rnorm(m, sd = 0.1)
}
X_mag[1, ] <- sin(2 * pi * t_grid) + 3  # Large vertical shift

fd_mag <- fdata(X_mag, argvals = t_grid)

# Visualize the magnitude outlier
plot(fd_mag) +
  labs(title = "Magnitude Outlier: Curve 1 Shifted Up",
       subtitle = "Same shape as others, but at a different level")

out_mag <- outliers.depth.pond(fd_mag, nb = 1000, seed = 123)
cat("Detected magnitude outlier:", out_mag$outliers, "\n")
#> Detected magnitude outlier: 1

Shape Outliers

Curves with different patterns but similar overall level:

# Create clean data with just a shape outlier
X_shape <- matrix(0, n, m)
for (i in 1:n) {
  X_shape[i, ] <- sin(2 * pi * t_grid) + rnorm(m, sd = 0.1)
}
X_shape[1, ] <- -sin(2 * pi * t_grid)  # Inverted (phase-shifted by pi)

fd_shape <- fdata(X_shape, argvals = t_grid)

# Visualize the shape outlier
plot(fd_shape) +
  labs(title = "Shape Outlier: Curve 1 Has Inverted Pattern",
       subtitle = "Same amplitude and level, but opposite phase")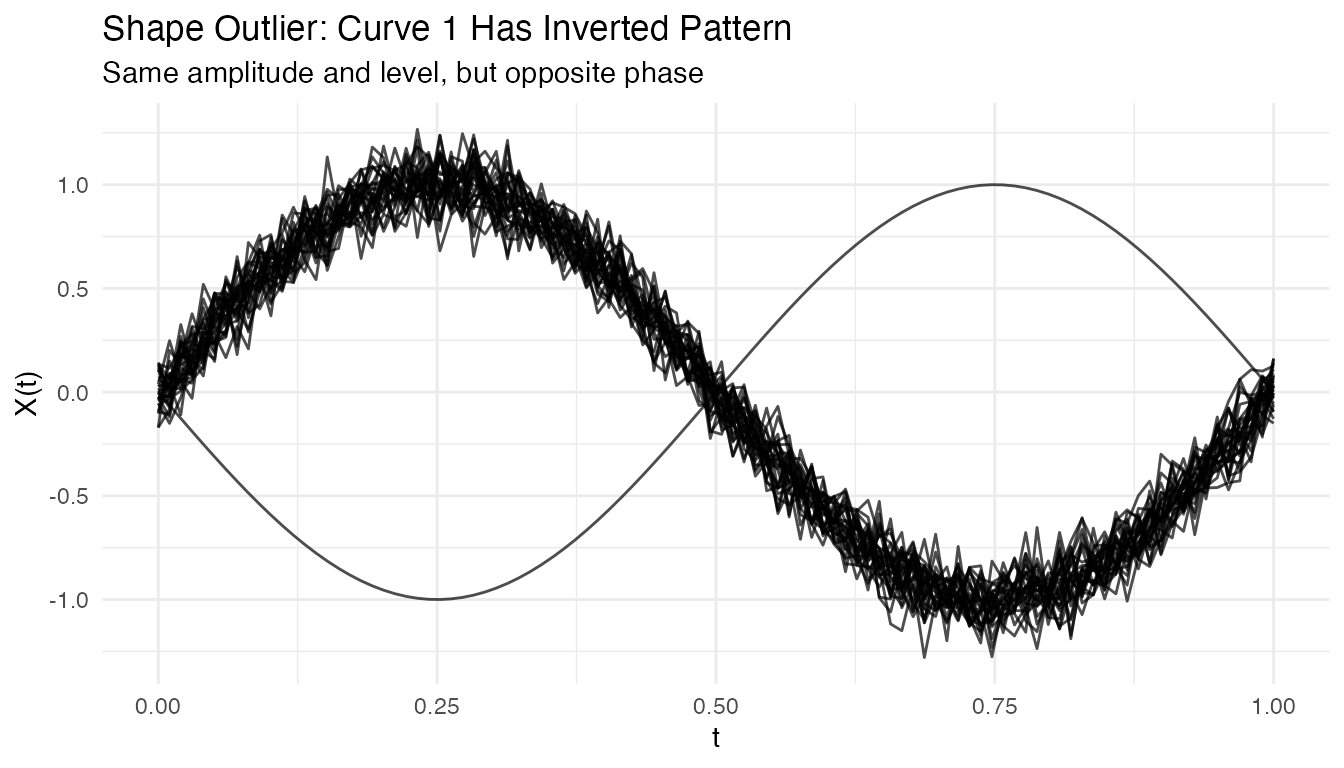

out_shape <- outliers.depth.pond(fd_shape, nb = 1000, seed = 123)
cat("Detected shape outlier:", out_shape$outliers, "\n")
#> Detected shape outlier: 1

Amplitude Outliers

Curves with unusual amplitude (larger or smaller scale):

# Create clean data with just an amplitude outlier
X_amp <- matrix(0, n, m)
for (i in 1:n) {
  X_amp[i, ] <- sin(2 * pi * t_grid) + rnorm(m, sd = 0.1)
}
X_amp[1, ] <- 3 * sin(2 * pi * t_grid)  # 3x larger amplitude

fd_amp <- fdata(X_amp, argvals = t_grid)

# Visualize the amplitude outlier
plot(fd_amp) +
  labs(title = "Amplitude Outlier: Curve 1 Has 3x Larger Scale",
       subtitle = "Same shape and center, but much larger oscillations")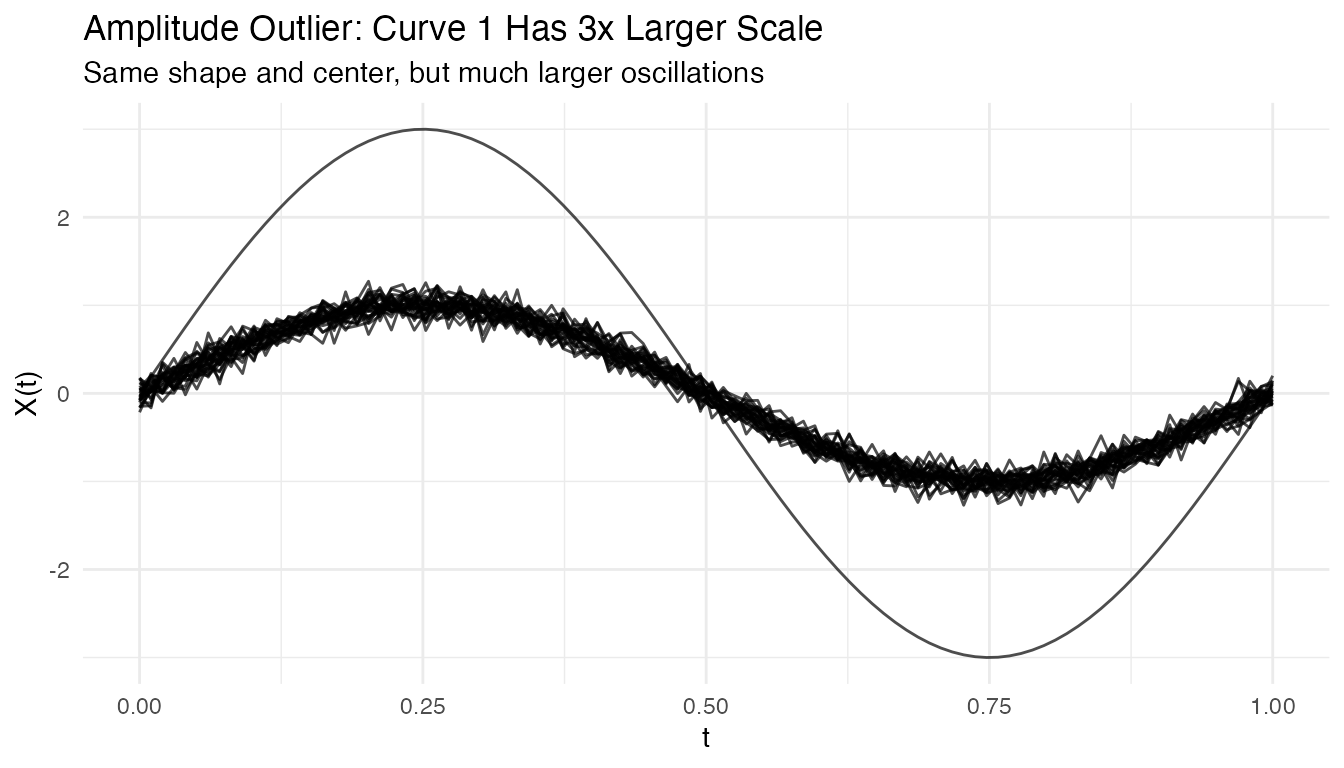

out_amp <- outliers.depth.pond(fd_amp, nb = 1000, seed = 123)
cat("Detected amplitude outlier:", out_amp$outliers, "\n")
#> Detected amplitude outlier: 1

Tuning Parameters

Number of Bootstrap Samples

More bootstrap samples give more stable results but take longer:

# Compare with different nb values
out_nb50 <- outliers.depth.pond(fd, nb = 50, seed = 123)
out_nb200 <- outliers.depth.pond(fd, nb = 200, seed = 123)

cat("nb=50 outliers:", out_nb50$outliers, "\n")
#> nb=50 outliers: 1 2 3
cat("nb=200 outliers:", out_nb200$outliers, "\n")
#> nb=200 outliers: 1 2 3

Trim Proportion

For outliers.depth.trim, the trim proportion controls sensitivity:

# More aggressive trimming
out_trim05 <- outliers.depth.trim(fd, trim = 0.05, seed = 123)
out_trim20 <- outliers.depth.trim(fd, trim = 0.2, seed = 123)

cat("trim=0.05 outliers:", out_trim05$outliers, "\n")
#> trim=0.05 outliers: 1 3
cat("trim=0.20 outliers:", out_trim20$outliers, "\n")
#> trim=0.20 outliers: 1 2 3 10 29 30

Handling High Contamination

When outlier contamination is high, use robust methods:

# Create data with 20% outliers
X_contam <- X
n_outliers <- 6
for (i in 1:n_outliers) {
  X_contam[i, ] <- sin(2 * pi * t_grid) + rnorm(1, 0, 2)
}

fd_contam <- fdata(X_contam, argvals = t_grid)

# Depth-trim with higher trim proportion
out_contam <- outliers.depth.trim(fd_contam, trim = 0.2, seed = 123)
cat("Detected outliers:", out_contam$outliers, "\n")
#> Detected outliers: 1 2 3 4 5 6
cat("True outliers: 1-6\n")
#> True outliers: 1-6

Visualizing Depth Distribution

# Compute depths
depths <- depth.FM(fd)

# Create histogram
library(ggplot2)
df_depths <- data.frame(
  curve = 1:n,
  depth = depths,
  type = ifelse(1:n %in% c(1, 2, 3), "Outlier", "Normal")
)

ggplot(df_depths, aes(x = depth, fill = type)) +
  geom_histogram(bins = 10, alpha = 0.7, position = "identity") +
  labs(title = "Distribution of Functional Depths",
       x = "Depth", y = "Count", fill = "") +
  theme_minimal()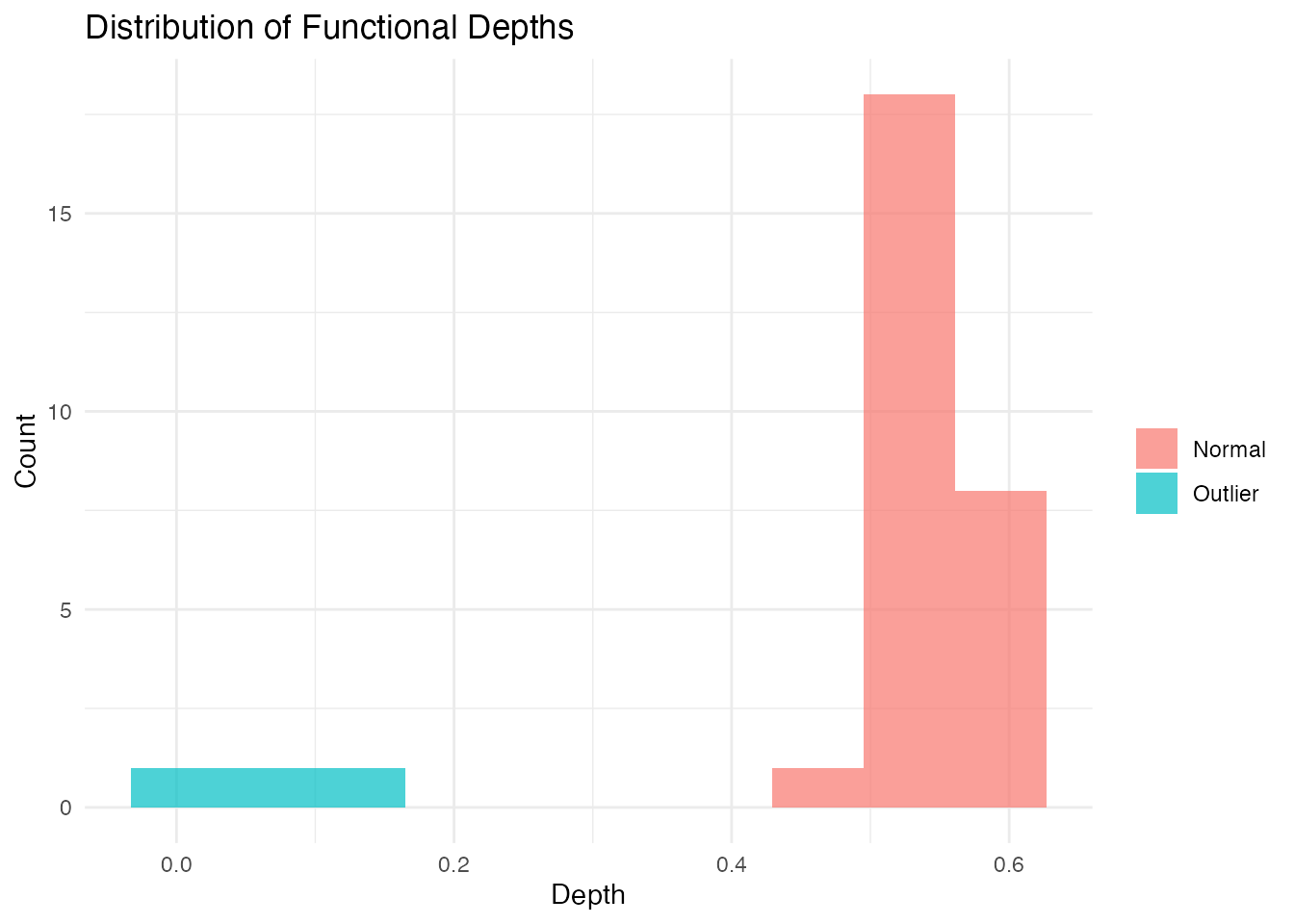

Performance

The LRT method uses a parallel Rust backend for speed:

# Benchmark with larger dataset
X_large <- matrix(rnorm(200 * 100), 200, 100)
fd_large <- fdata(X_large)

system.time(outliers.lrt(fd_large, nb = 200, seed = 123))
#>    user  system elapsed
#>   0.456   0.000   0.123

Outliergram and MS-Plot

For visual outlier detection, fdars provides two powerful diagnostic plots.

The Outliergram

The outliergram plots the Modified Epigraph Index (MEI) against Modified Band Depth (MBD):

og <- outliergram(fd)
plot(og)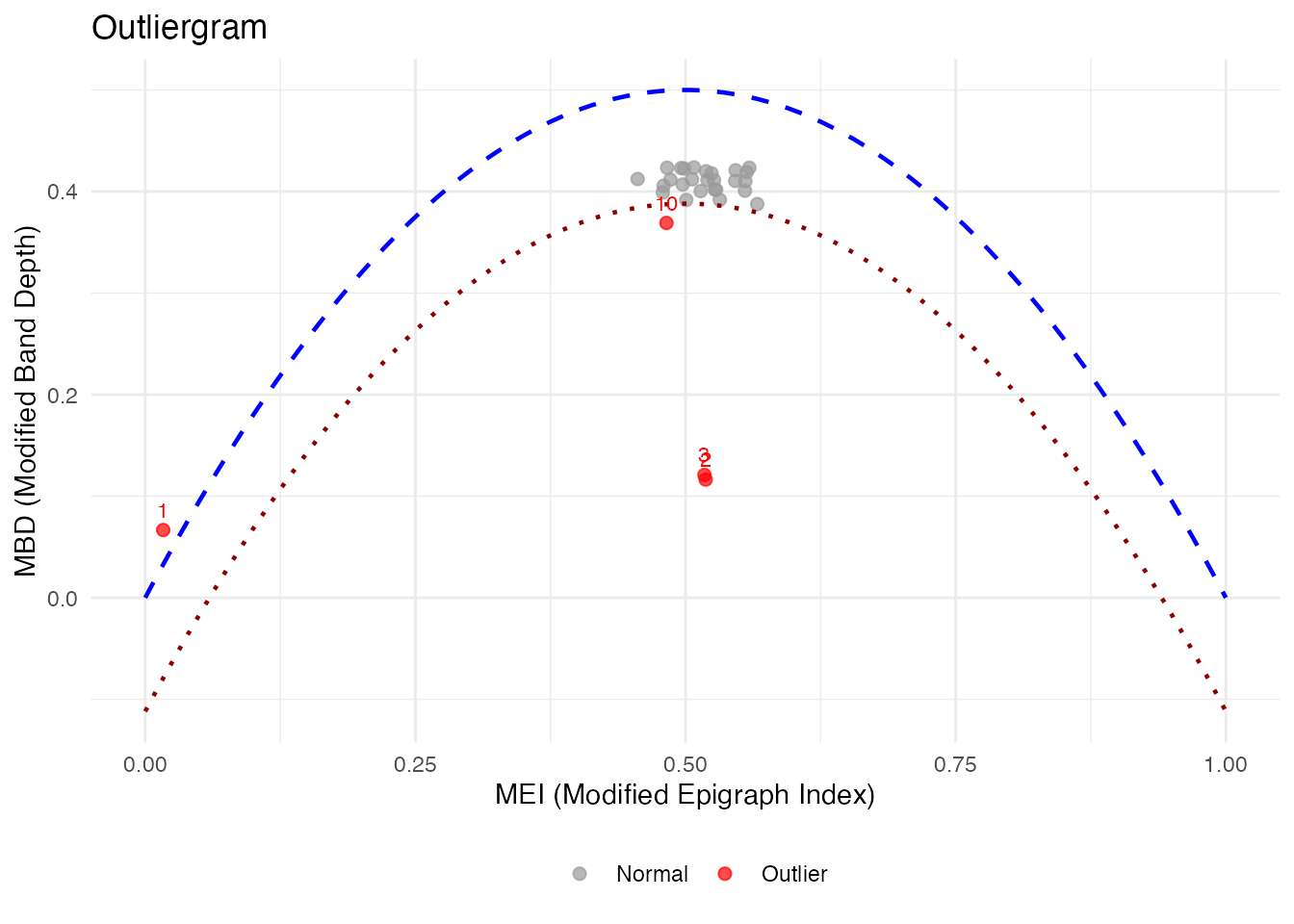

How to read the outliergram:

Position	MEI (X-axis)	MBD (Y-axis)	Interpretation
Bottom-left	Low	Low	Extreme outlier (unusual shape AND position)
Bottom-right	High	Low	Magnitude outlier (shifted up/down)
Top-left	Low	High	Shape outlier (unusual pattern, typical level)
Top-right	High	High	Normal curve (typical shape and position)

The parabolic boundary marks the theoretical limit for non-outlying curves. Points below this boundary are flagged as outliers.

The Magnitude-Shape Plot (MS-Plot)

The MS-plot separates magnitude outlyingness from shape outlyingness:

ms <- magnitudeshape(fd)
plot(ms)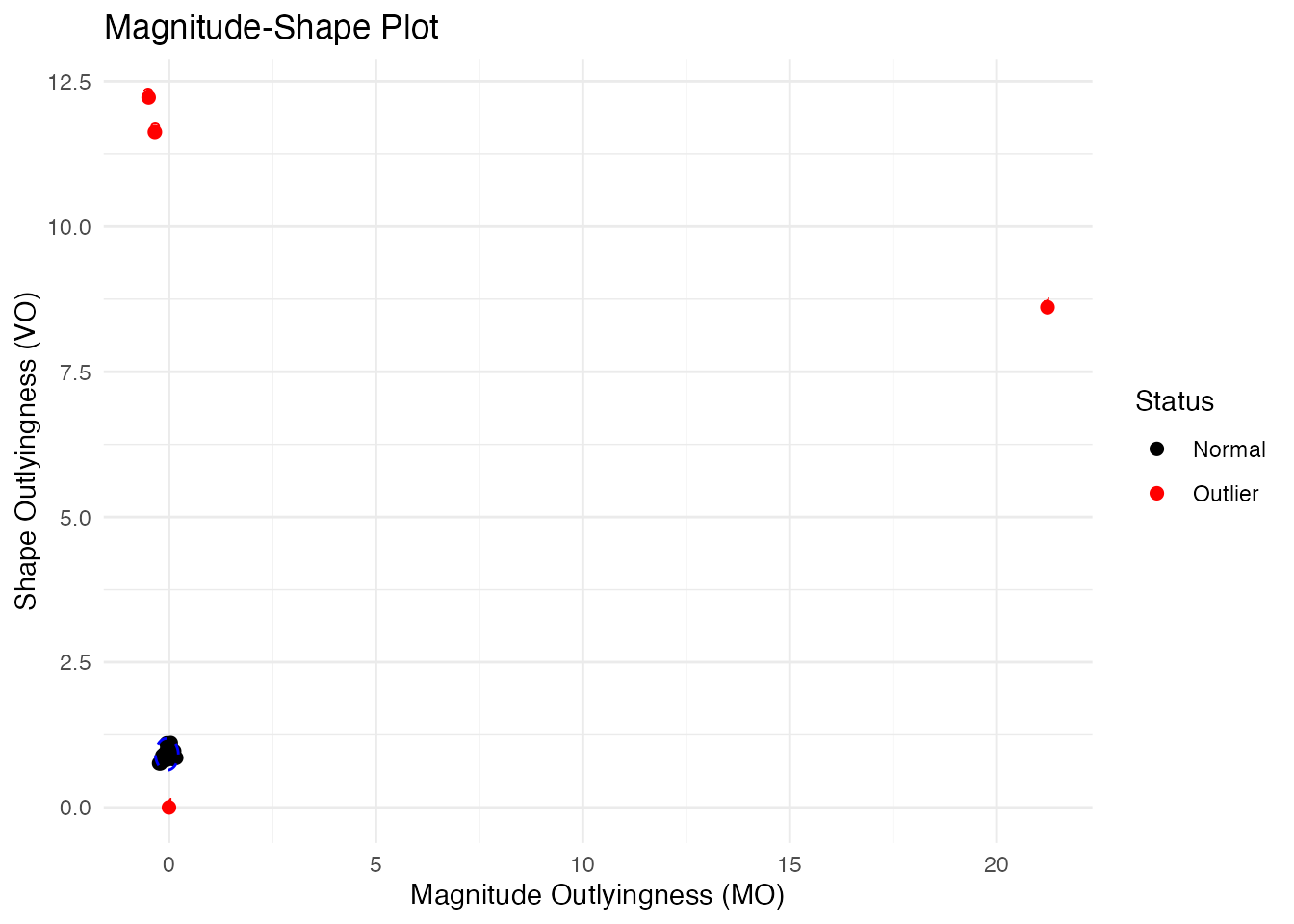

How to read the MS-plot:

Quadrant	Magnitude Outlyingness	Shape Outlyingness	Type
Bottom-left	Low	Low	Normal curve
Bottom-right	High	Low	Magnitude outlier only
Top-left	Low	High	Shape outlier only
Top-right	High	High	Combined outlier (both types)

The MS-plot is particularly useful when you want to understand why a curve is an outlier - is it because of its level (magnitude) or its pattern (shape)?

Labeling Outliers by ID or Metadata

When fdata has IDs or metadata, you can label outliers in plots:

# Create fdata with IDs and metadata
meta <- data.frame(
  subject = paste0("S", sprintf("%02d", 1:n)),
  group = rep(c("A", "B"), length.out = n)
)
fd_labeled <- fdata(X, argvals = t_grid,
                    id = paste0("patient_", 1:n),
                    metadata = meta)

# Outliergram with patient IDs
og_labeled <- outliergram(fd_labeled)
plot(og_labeled, label = "id")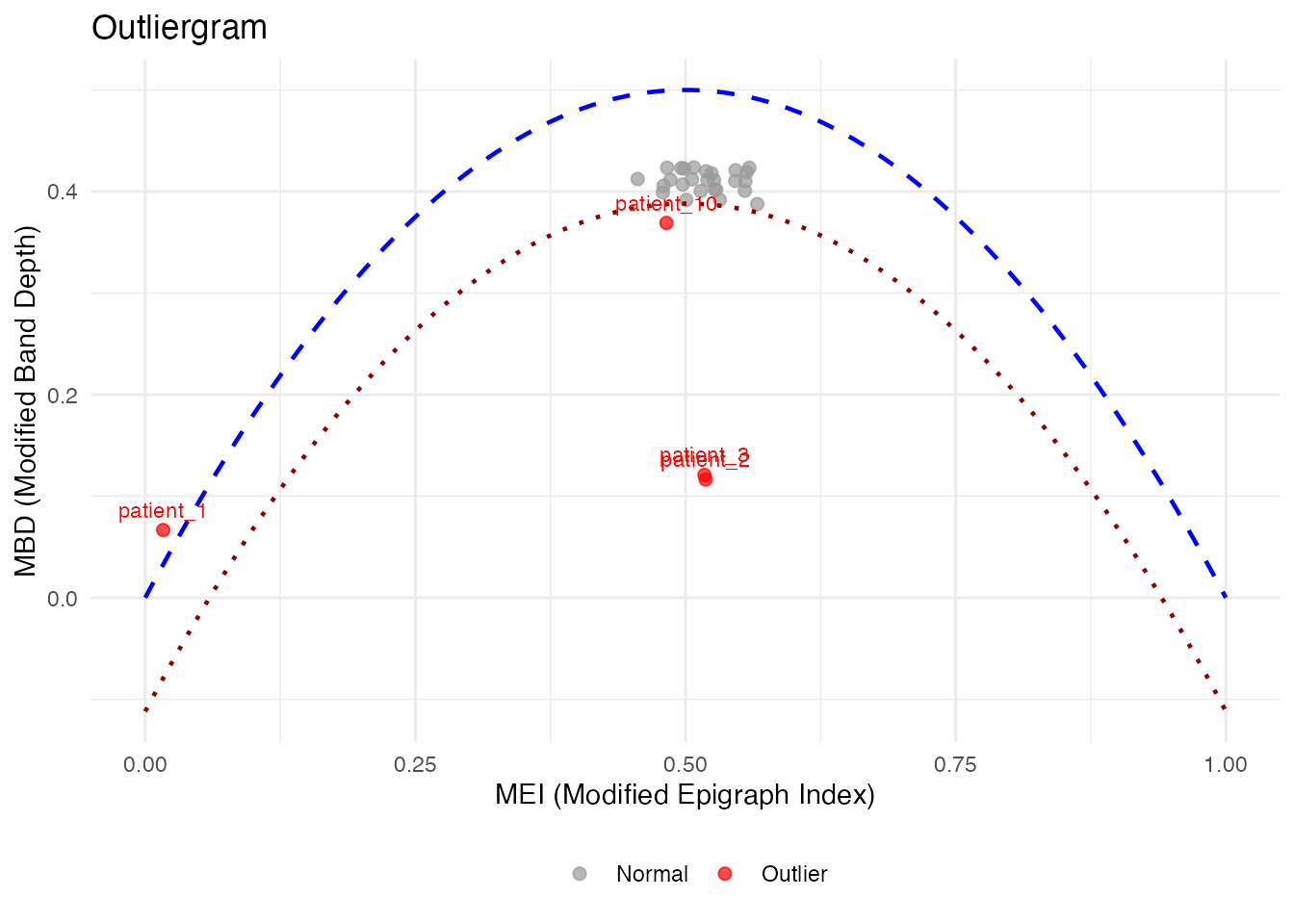


# Or with metadata column
plot(og_labeled, label = "subject")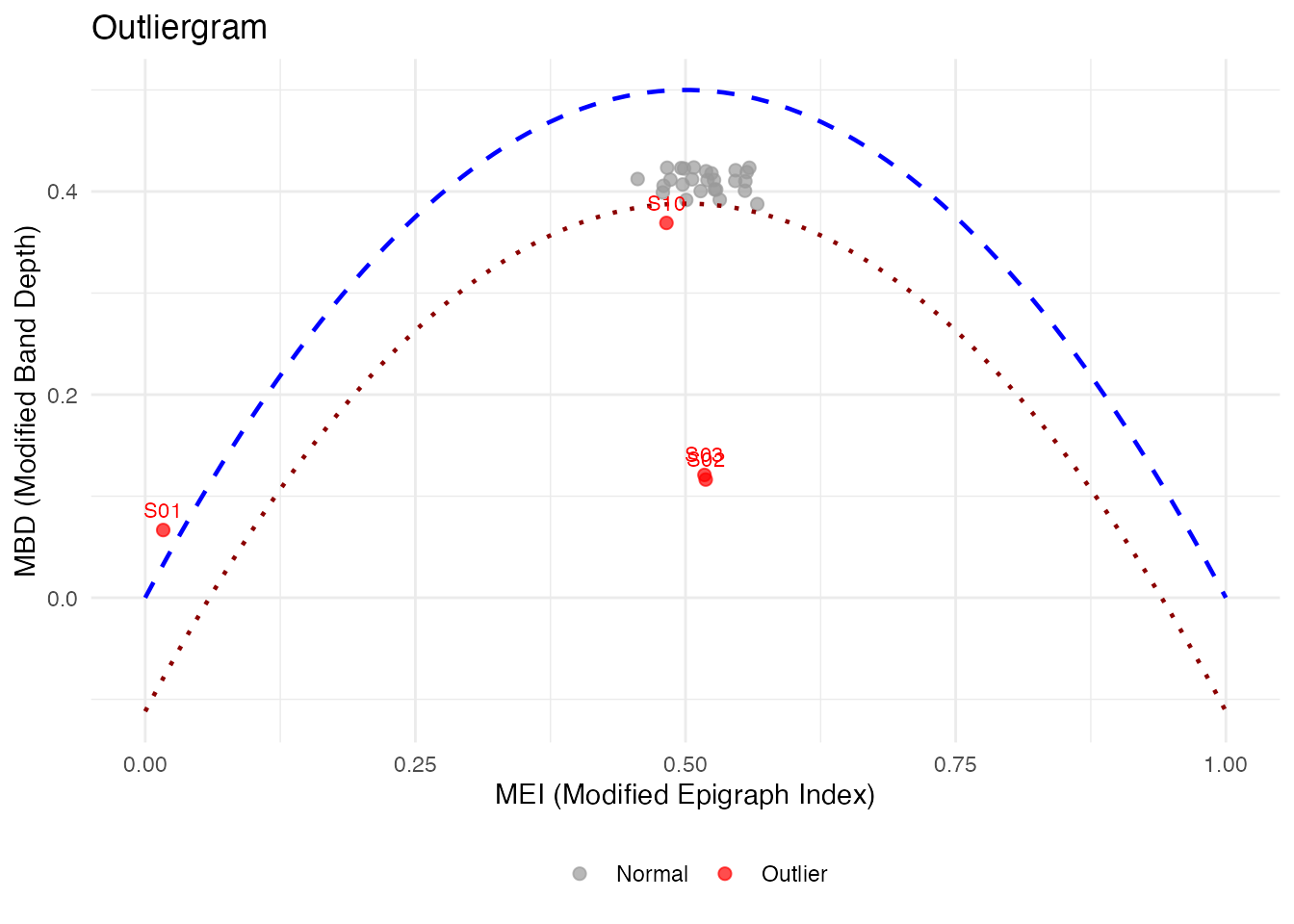


# Label ALL points, not just outliers
plot(og_labeled, label = "id", label_all = TRUE)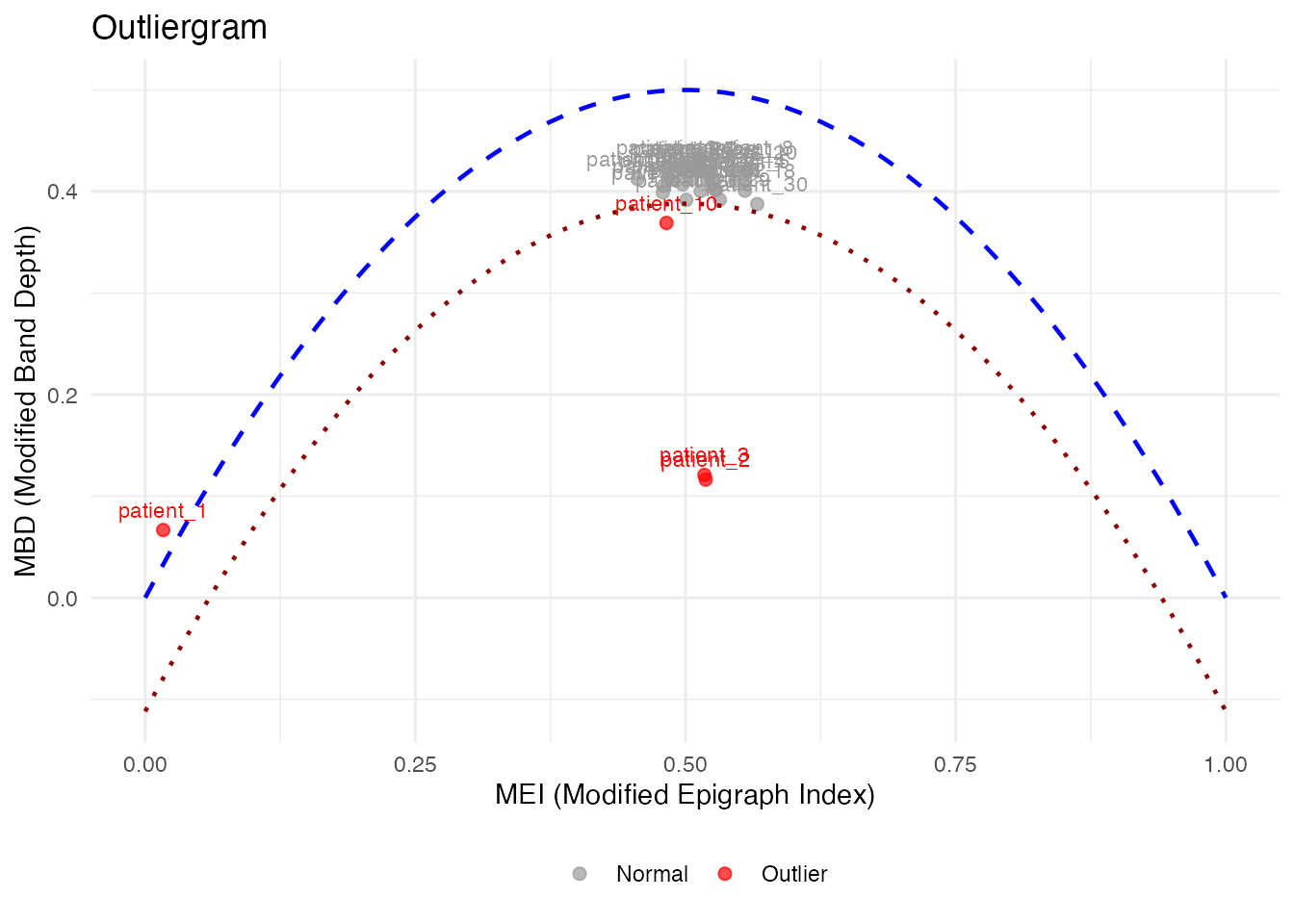

# magnitudeshape with custom labels
magnitudeshape(fd_labeled, label = "subject")

Method Selection Guide

Method	Best For	Sensitivity
depth.pond	General purpose	Moderate
depth.trim	Known contamination rate	Controllable
LRT	Magnitude outliers	High
outliergram	Shape outliers	Visual
magnitudeshape	Both magnitude & shape	Visual

Best Practices

Start with visualization: Plot the data to understand outlier types
Try multiple methods: Different methods catch different outliers
Use sufficient bootstrap samples: At least 100 for stable results
Consider domain knowledge: Some “outliers” may be valid observations
Validate findings: Check detected outliers make sense contextually

References

Febrero, M., Galeano, P., and González-Manteiga, W. (2008). Outlier detection in functional data by depth measures, with application to identify abnormal NOx levels. Environmetrics, 19(4), 331-345.
Hyndman, R.J. and Shang, H.L. (2010). Rainbow plots, bagplots, and boxplots for functional data. Journal of Computational and Graphical Statistics, 19(1), 29-45.