Computes the Brownian motion (Wiener process) covariance function: $$k(s, t) = \sigma^2 \min(s, t)$$
Details
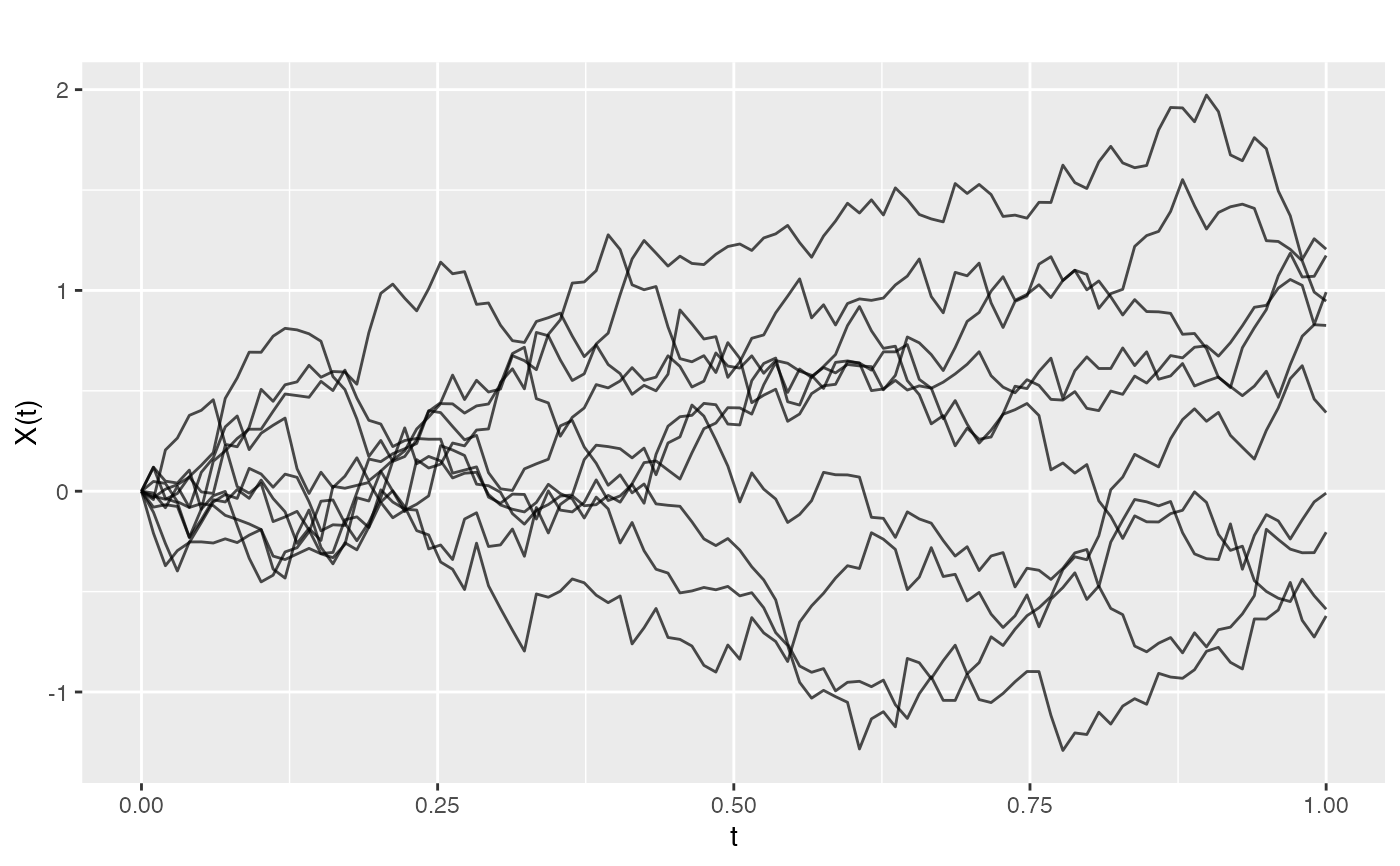
The Brownian motion covariance produces sample paths that start at 0 and have independent increments. The covariance between two points equals the variance times the minimum of their positions.
This covariance is only defined for 1D domains starting at 0.
Examples
# Generate Brownian motion paths
cov_func <- kernel.brownian(variance = 1)
t <- seq(0, 1, length.out = 100)
fd <- make.gaussian.process(n = 10, t = t, cov = cov_func)
plot(fd)