Generates functional data samples from a Gaussian process with the specified mean and covariance functions.
Usage
make.gaussian.process(n, t, cov = kernel.gaussian(), mean = 0, seed = NULL)Arguments
- n
Number of samples to generate.
- t
Evaluation points (vector for 1D, list of two vectors for 2D).
- cov
Covariance function (from
kernel.gaussian,kernel.matern, etc.).- mean
Mean function. Can be a scalar (default 0), a vector of length equal to the number of evaluation points, or a function.
- seed
Optional random seed for reproducibility.
Details
This function generates samples from a Gaussian process with the specified covariance structure. The samples are generated by computing the Cholesky decomposition of the covariance matrix and multiplying by standard normal random variables.
For 2D functional data, pass t as a list of two vectors representing
the grid in each dimension.
Examples
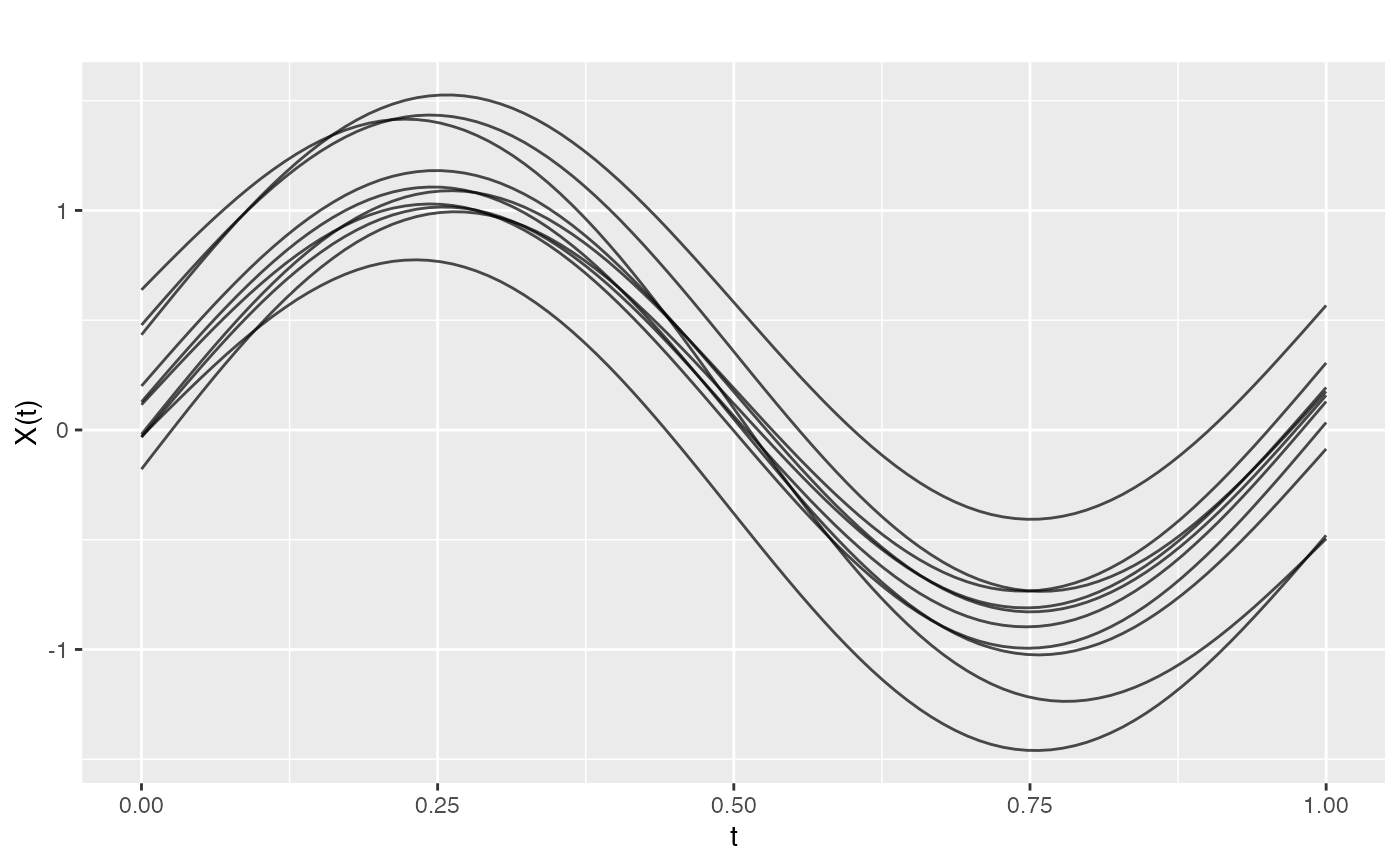
# Generate smooth GP samples with Gaussian covariance
t <- seq(0, 1, length.out = 100)
fd <- make.gaussian.process(n = 20, t = t,
cov = kernel.gaussian(length_scale = 0.2),
seed = 42)
plot(fd)
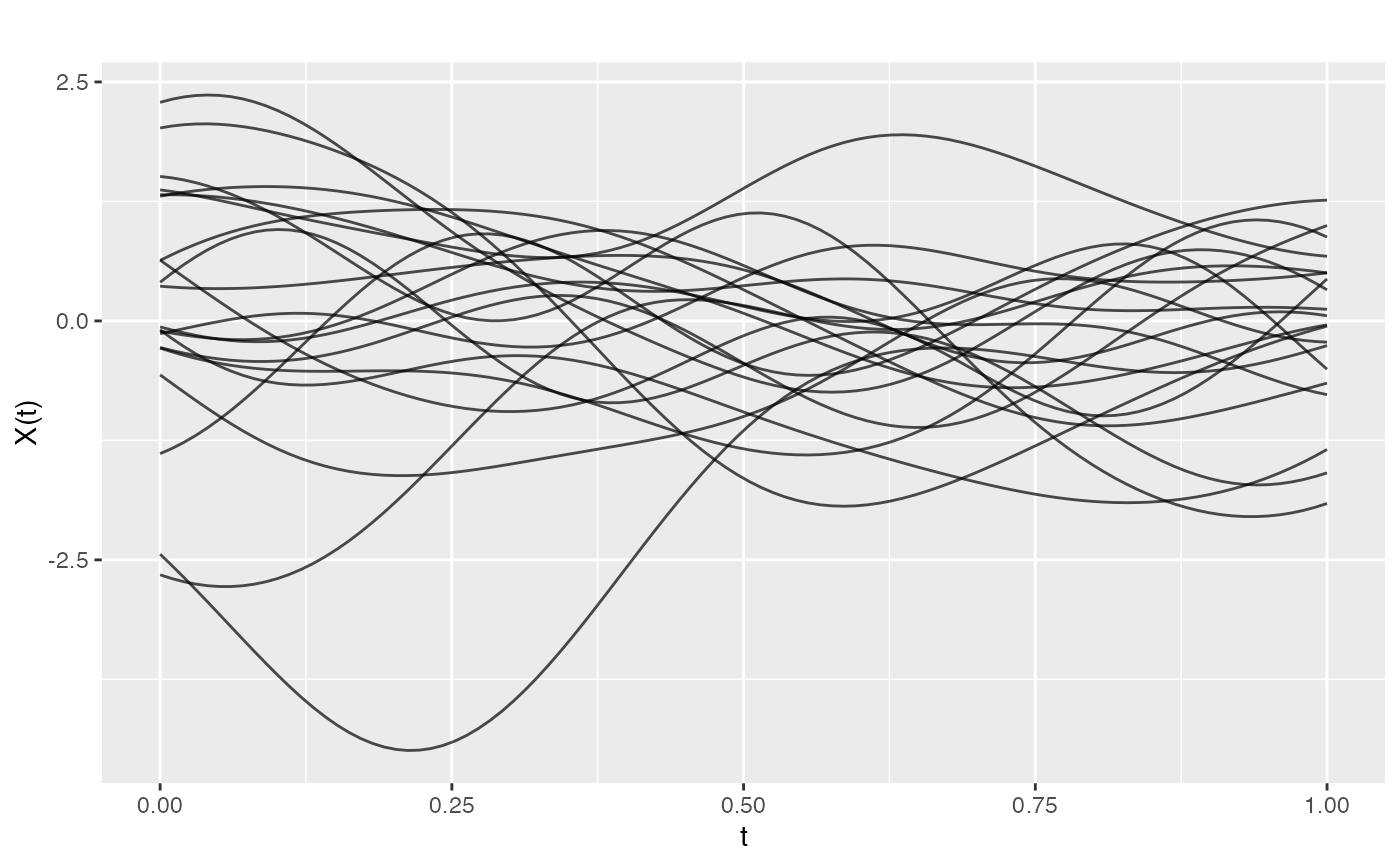 # Generate rough GP samples with exponential covariance
fd_rough <- make.gaussian.process(n = 20, t = t,
cov = kernel.exponential(length_scale = 0.1),
seed = 42)
plot(fd_rough)
# Generate rough GP samples with exponential covariance
fd_rough <- make.gaussian.process(n = 20, t = t,
cov = kernel.exponential(length_scale = 0.1),
seed = 42)
plot(fd_rough)
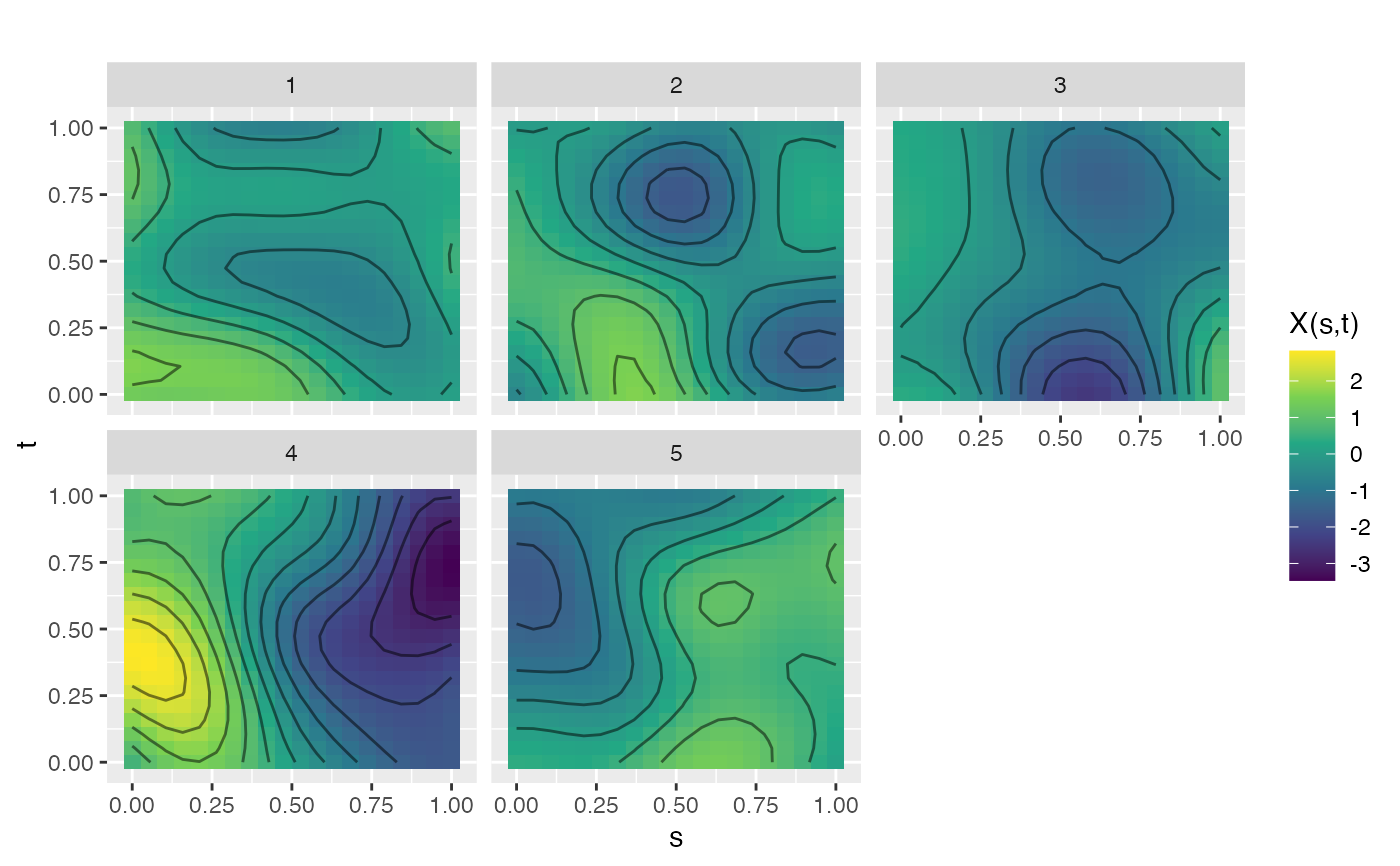
 # Generate 2D GP samples (surfaces)
s <- seq(0, 1, length.out = 20)
t2 <- seq(0, 1, length.out = 20)
fd2d <- make.gaussian.process(n = 5, t = list(s, t2),
cov = kernel.gaussian(length_scale = 0.3),
seed = 42)
plot(fd2d)
# Generate 2D GP samples (surfaces)
s <- seq(0, 1, length.out = 20)
t2 <- seq(0, 1, length.out = 20)
fd2d <- make.gaussian.process(n = 5, t = list(s, t2),
cov = kernel.gaussian(length_scale = 0.3),
seed = 42)
plot(fd2d)
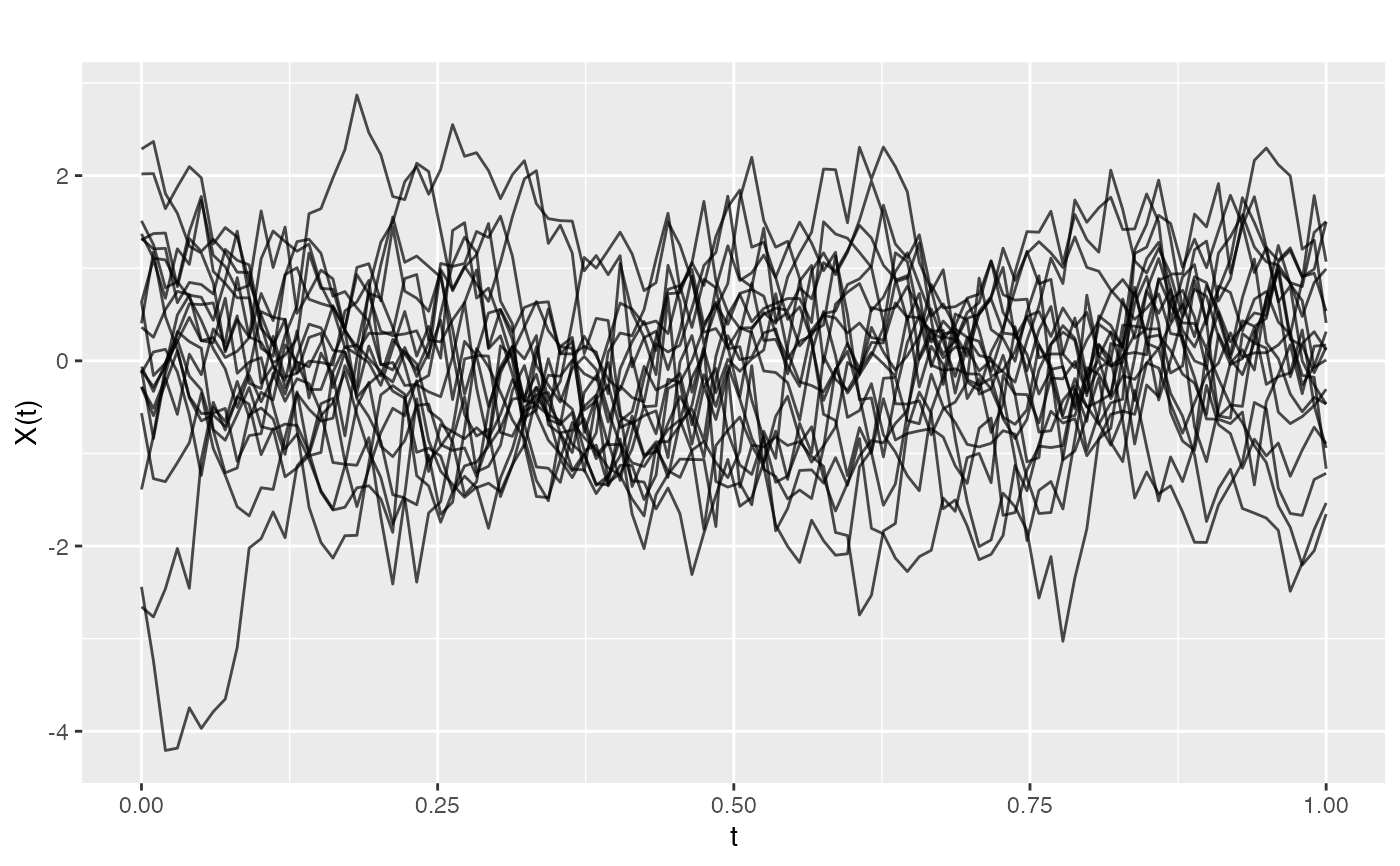
 # Generate GP with non-zero mean
mean_func <- function(t) sin(2 * pi * t)
fd_mean <- make.gaussian.process(n = 10, t = t,
cov = kernel.gaussian(variance = 0.1),
mean = mean_func, seed = 42)
plot(fd_mean)
# Generate GP with non-zero mean
mean_func <- function(t) sin(2 * pi * t)
fd_mean <- make.gaussian.process(n = 10, t = t,
cov = kernel.gaussian(variance = 0.1),
mean = mean_func, seed = 42)
plot(fd_mean)