Estimate Mean Function for Irregular Data

Estimates the mean function from irregularly sampled functional data.

Usage

# S3 method for class 'irregFdata'
mean(
  x,
  argvals = NULL,
  method = c("basis", "kernel"),
  nbasis = 15,
  type = c("bspline", "fourier"),
  bandwidth = NULL,
  kernel = c("epanechnikov", "gaussian"),
  ...
)

Arguments

x

An object of class irregFdata.

argvals

Target grid for mean estimation. If NULL, uses a regular grid of 100 points.

method

Estimation method: "basis" (default, recommended) fits basis functions to each curve then averages; "kernel" uses Nadaraya-Watson kernel smoothing.

nbasis

Number of basis functions for method = "basis" (default 15).

type

Basis type for method = "basis": "bspline" (default) or "fourier".

bandwidth

Kernel bandwidth for method = "kernel". If NULL, uses range/10.

kernel

Kernel type for method = "kernel": "epanechnikov" (default) or "gaussian".

...

Additional arguments (ignored).

Value

An fdata object containing the estimated mean function.

Details

The "basis" method (default) works by:

1. Fitting basis functions to each curve via least squares

2. Reconstructing each curve on the target grid

3. Averaging the reconstructed curves

This approach preserves the functional structure and typically gives more accurate estimates than kernel smoothing.

The "kernel" method uses Nadaraya-Watson estimation, pooling all observations across curves. This is faster but may be less accurate for structured functional data.

Examples

t <- seq(0, 1, length.out = 100)
fd <- simFunData(n = 50, argvals = t, M = 5, seed = 42)
ifd <- sparsify(fd, minObs = 10, maxObs = 30, seed = 123)

# Recommended: basis method
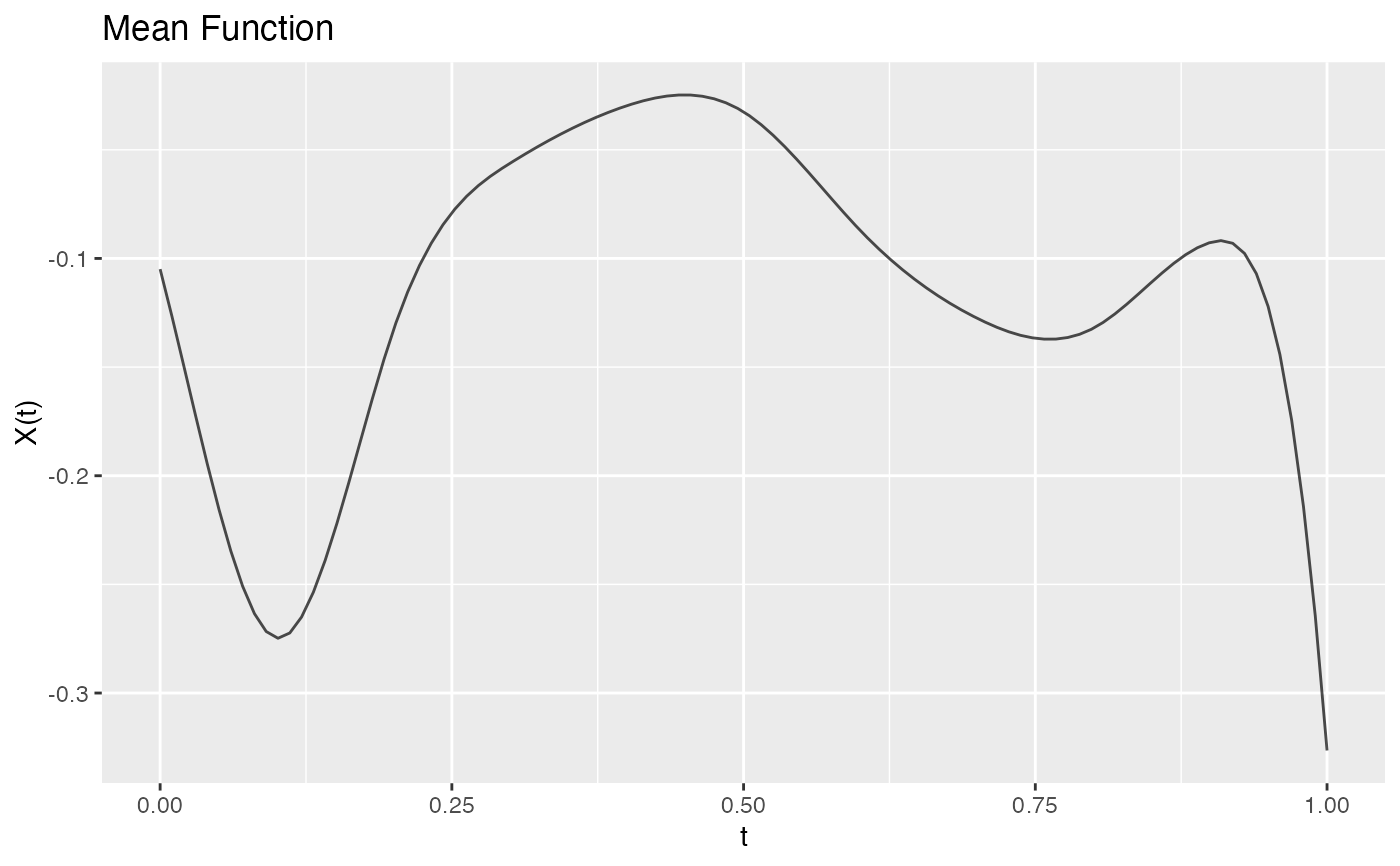
mean_fd <- mean(ifd)
plot(mean_fd, main = "Estimated Mean Function")


# Alternative: kernel method
mean_kernel <- mean(ifd, method = "kernel", bandwidth = 0.1)